THE PROBLEM WITH NUMBERS
There is a problem in how we learn to count. It is my view that a lot of people who ‘struggle with mathematics’ do so because it appears too abstract, almost unreasonably so. In learning our 1,2,3s we immediately associate numbers with the script that we use to represent those numbers – the very “1,2,3’s” we used above. This, to my mind, obfuscates a rather important aspect of numbers and that is how they interrelate. Below is one way I developed to enhance one’s intuition about numbers and I share in the hope that it will help others.
I also find that there is a certain simple beauty to it which I hope will help kindle a love of mathematics in anyone who cares to use it.
THE PROBLEM OF BASE COUNTING SYSTEMS
Mathematics has no intrinsic base system other than, arguably, that of the primorial base system or binary (to be discussed later). There have been countless counting systems throughout history (see here for a selection) but they are all abstractions of a sort and, to my mind at least, serve to confuse people as to what numbers are. This leads to various biases in our approach to numbers, for example, we find multiplying by ten easier and more natural than multiplying by seven. This is obviously merely an artefact of us using a decimal base counting system. However, this is just one example of such a bias and there are countless more. In the system below I hope to represent numbers as they stand in relation to other numbers regardless of the base system one chooses to use.

Setup: We define a number line, a single dimension in effect, along which we will count.
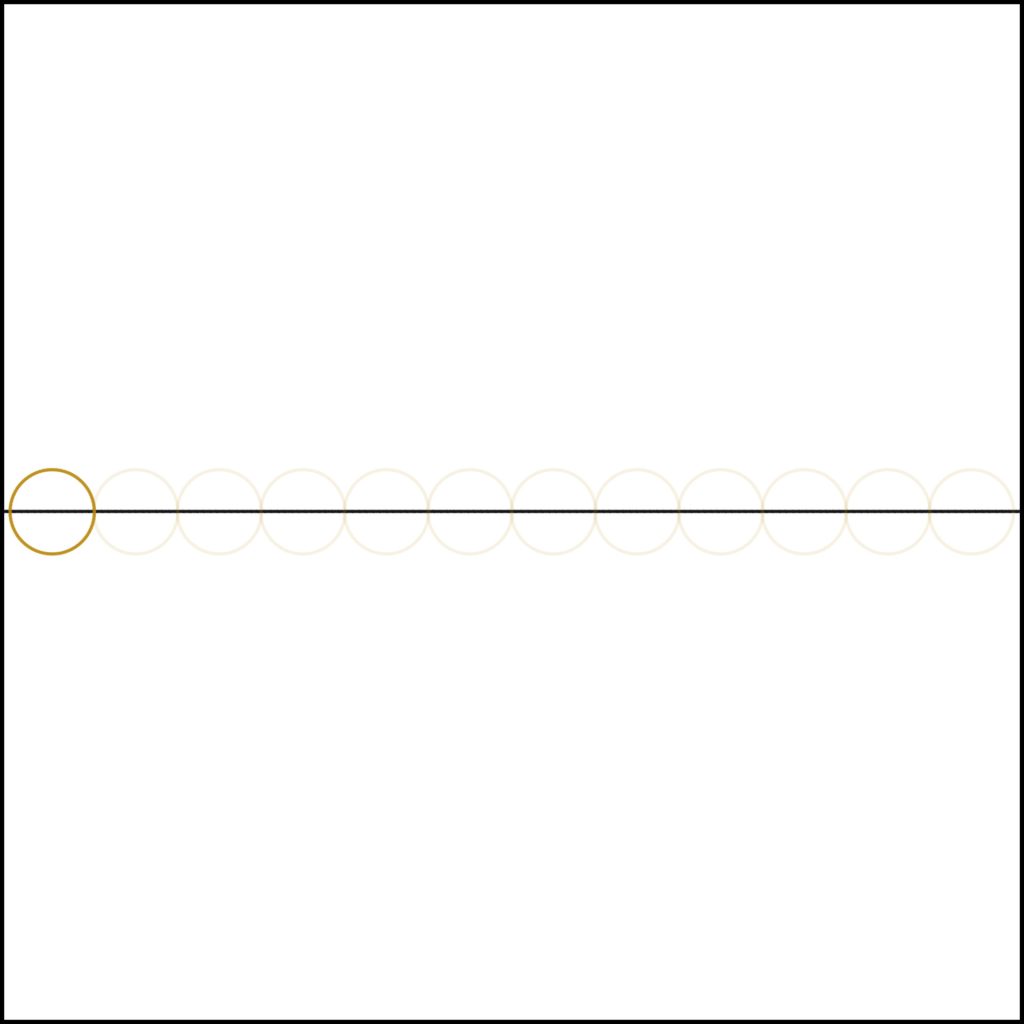
Step 1: We define the unit value.
Once this is done all other numbers to ∞ can be created by repeating this process (a simple one times table as represented by the ghost numbers).
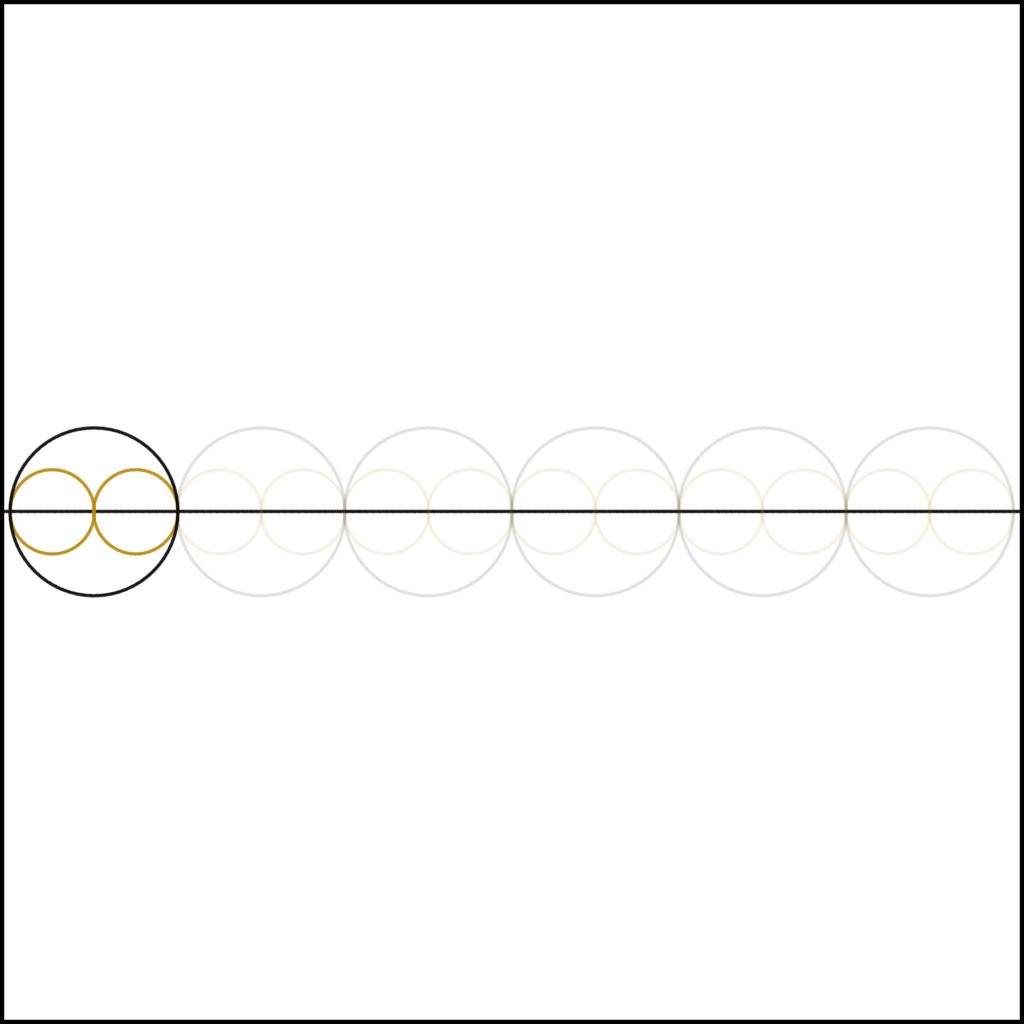
Step 2: We add one to the existing unit, creating two.
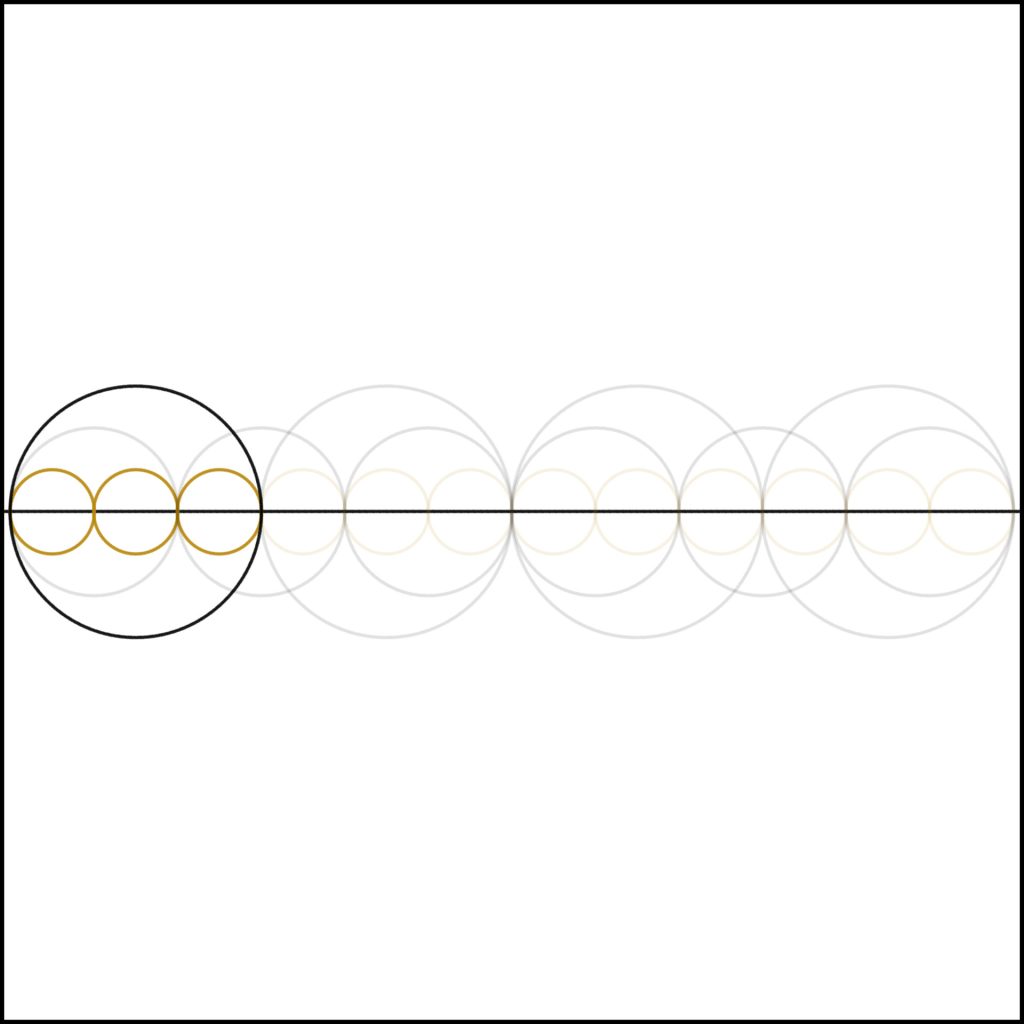
Step 3: We continue this process, adding one to two giving three.
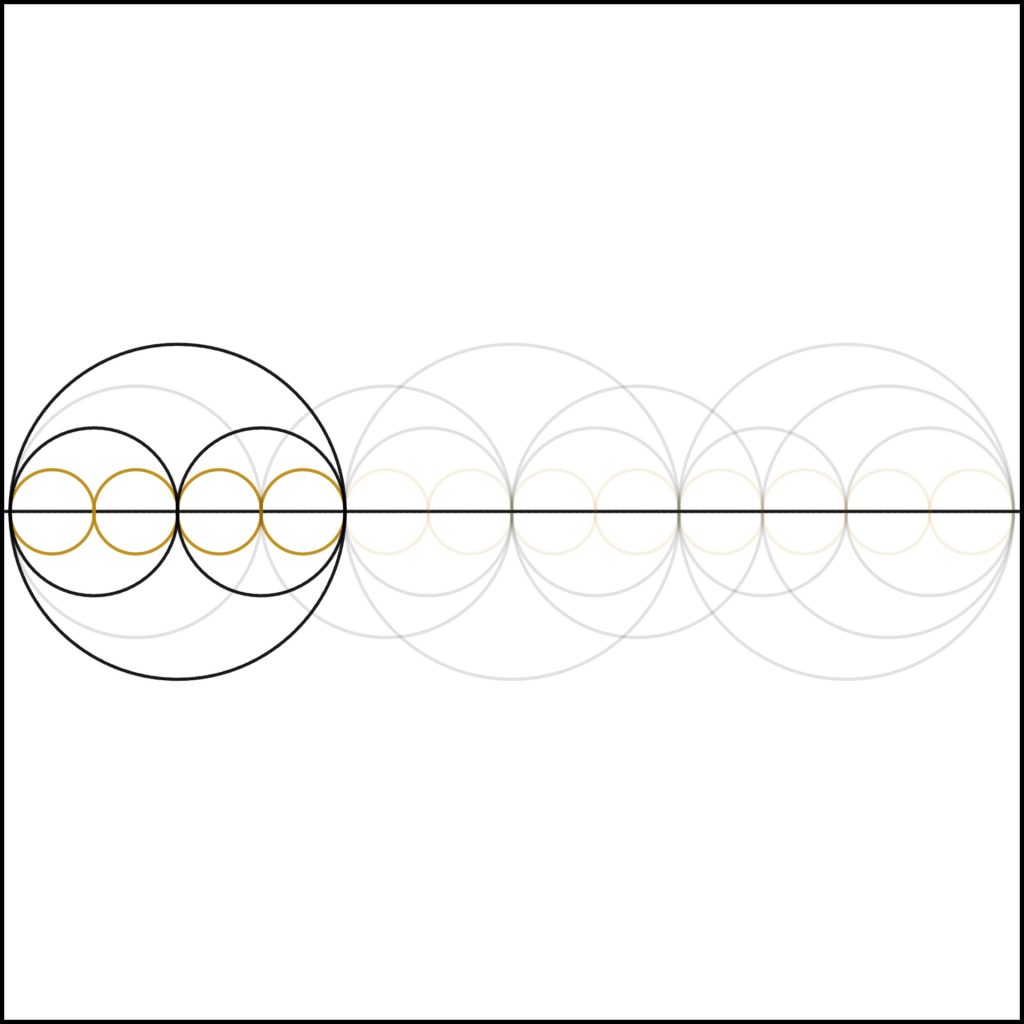
Step 4: As we add one to three we come to our first non-prime and square number. Notice simple self similarity, how the whole is divided in two and then those parts divided into the same structure.
From this image, and all that follow, it is self evident that 4 = 4 x 1 = 2 x 2.
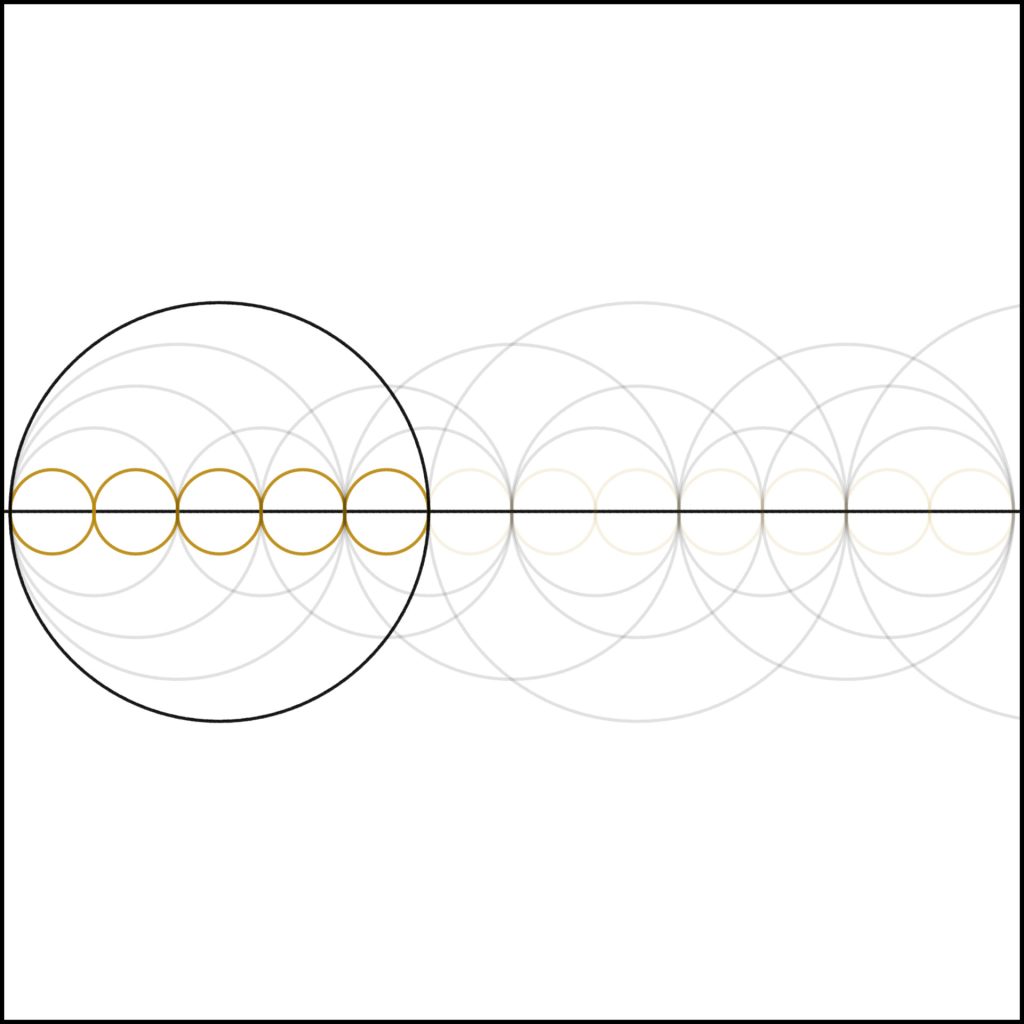
Step 5: As we add one to four, we come to five. Notice how the complexity of the number drops back to that of the single band of units. This is to be expected as 5 is, of course, prime.
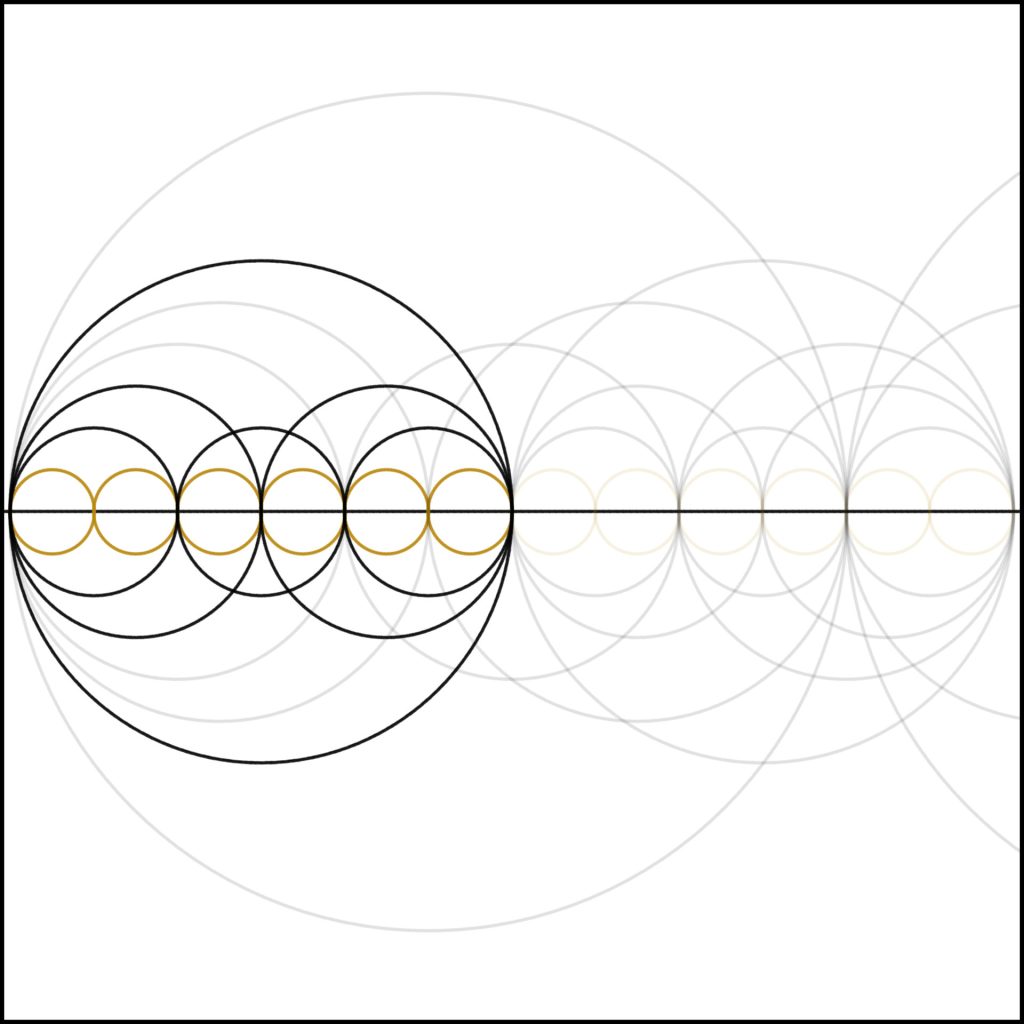
Step 6: As we add one to five creating six, we again see a relative explosion of structure within the number, similar to how we did in the case of 4. We can see the harmonics within it.
6 = 6 x 1 = 2 x 3 = 3 x 2.
As an interesting side point this is also the foundation for the yin-yang symbol (to be discussed elsewhere).
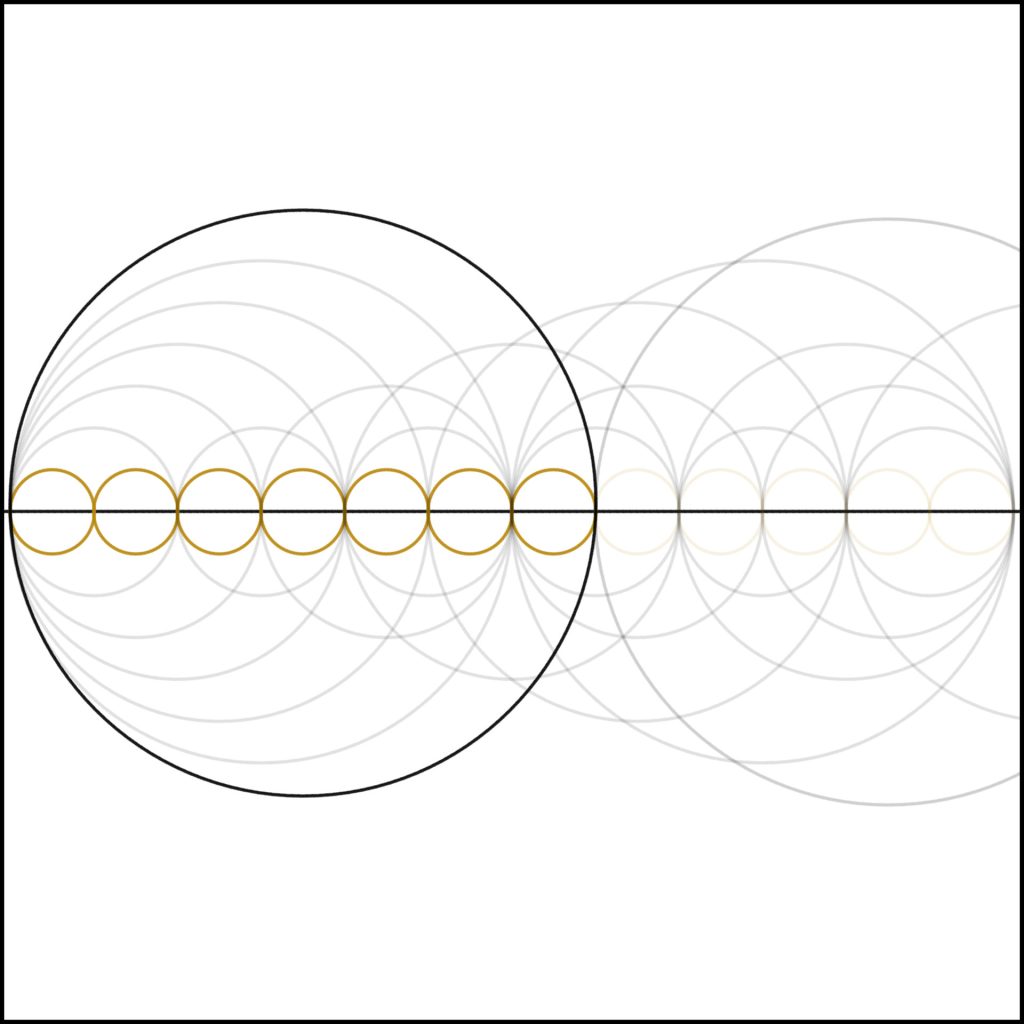
Step 7: As we continue, we come to 7. Notice the collapse in internal harmonics. Again, as a result of 7 being prime.
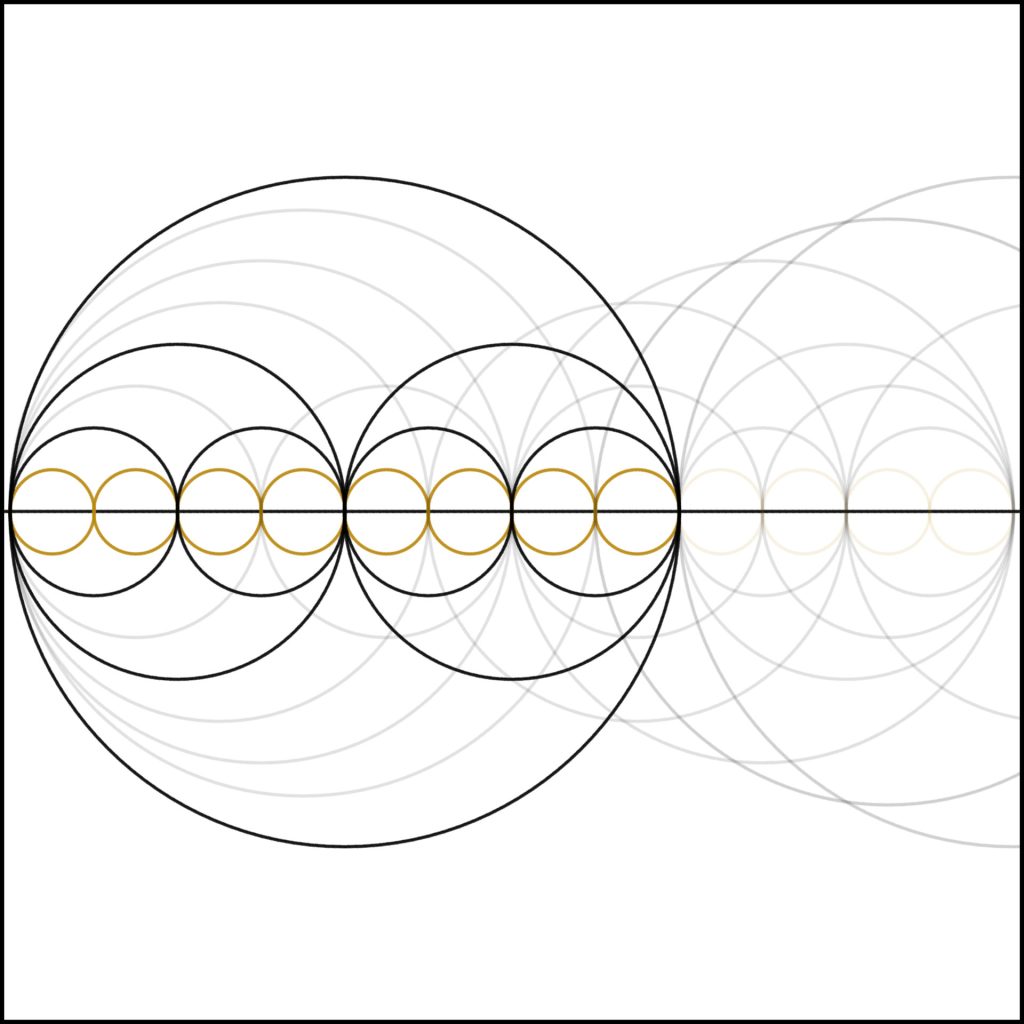
Step 8: We now come to 8, our first cube. We can clearly see the self-similarity three levels down. (2 is similar to 4 is similar to 8, the whole number, in structure)
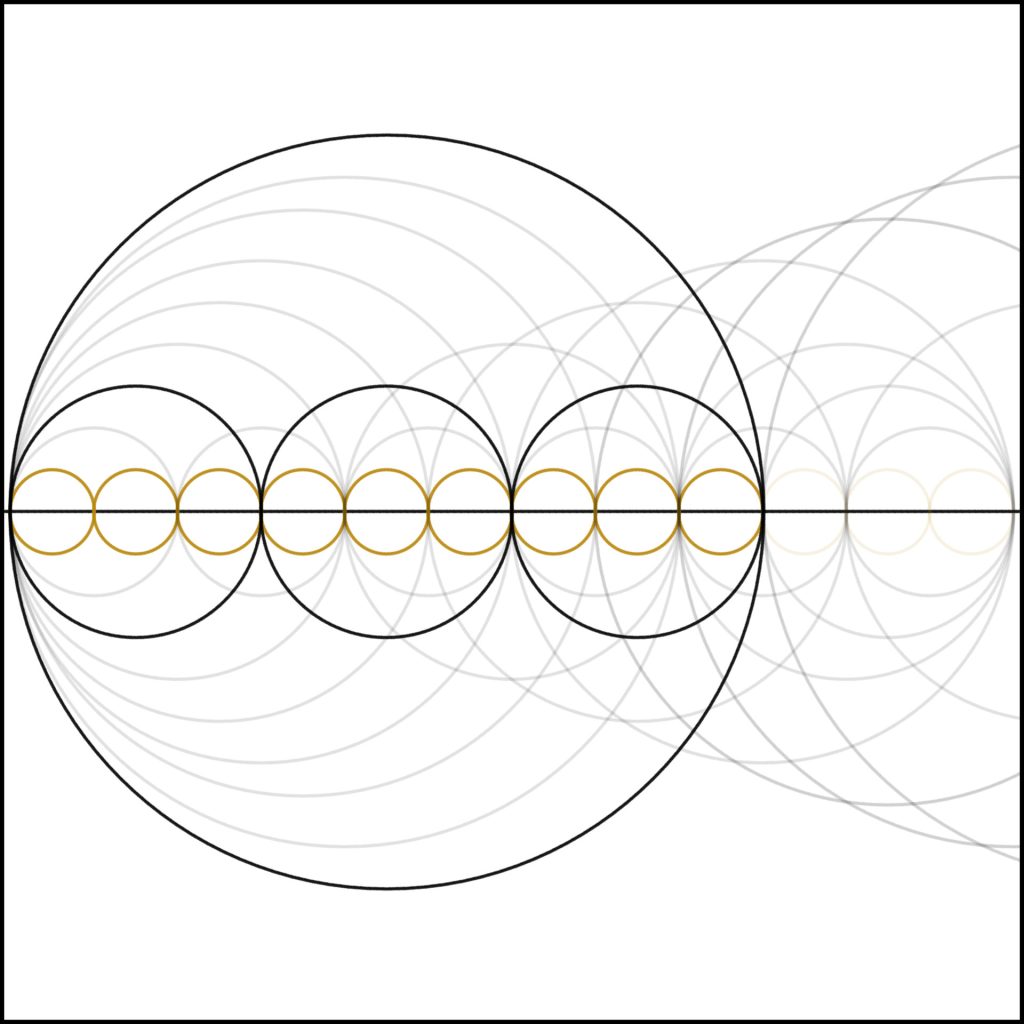
Step 9: Now we come to 9, our second square number. Notice again how clearly you can see the self-similar nature of the nine dividing into three and those threes also diving into threes.
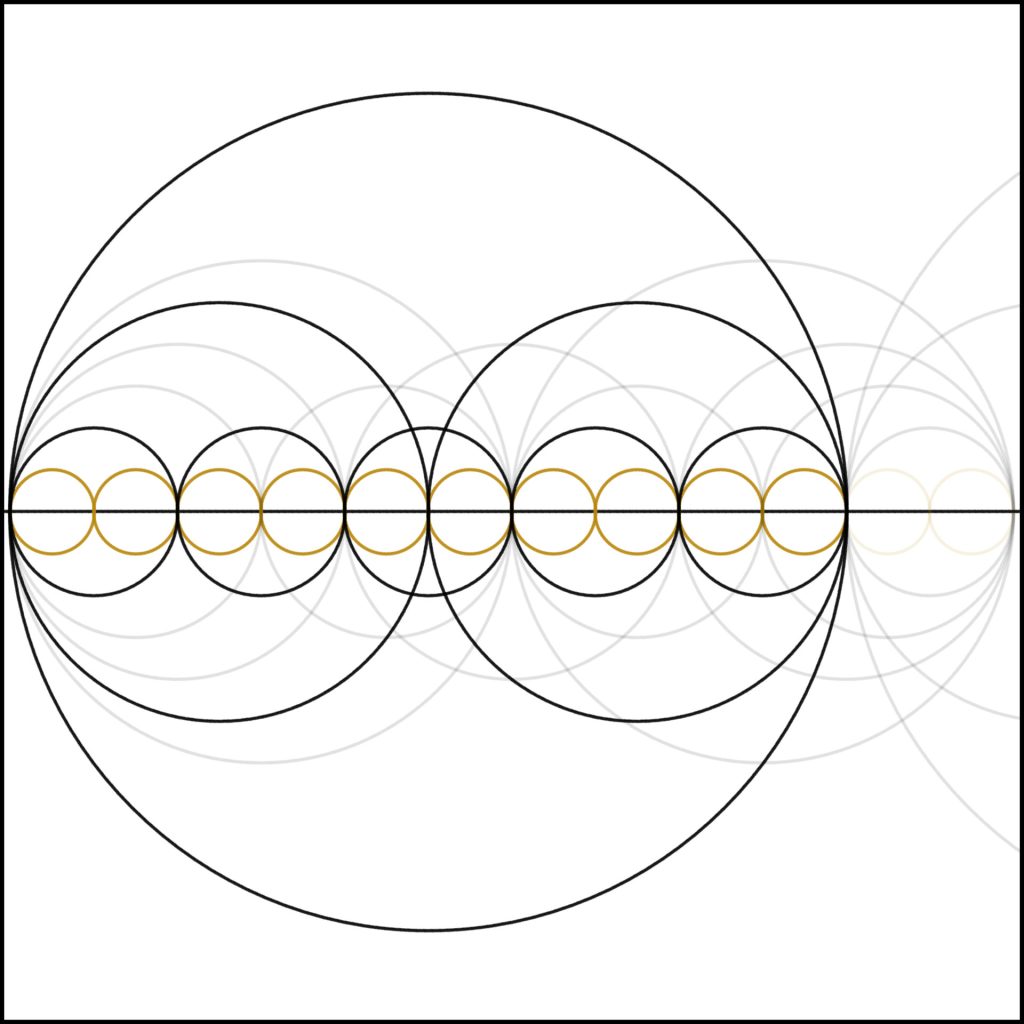
Step 10: At 10, as with 6, we find a simple composite number. Again, notice the superficial similarity between these two numbers.
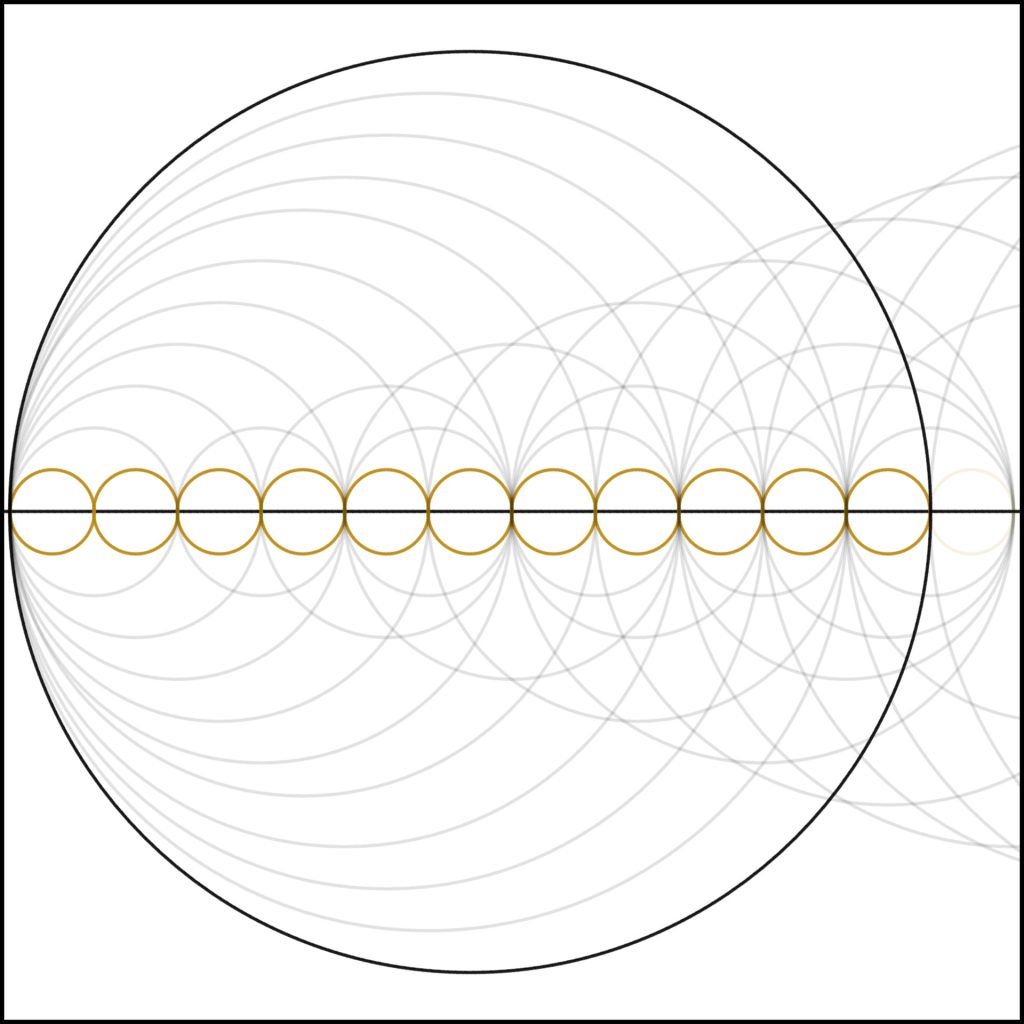
Step 11: At 11 we see again see the familiar collapse of internal complexity we see with all prime numbers.
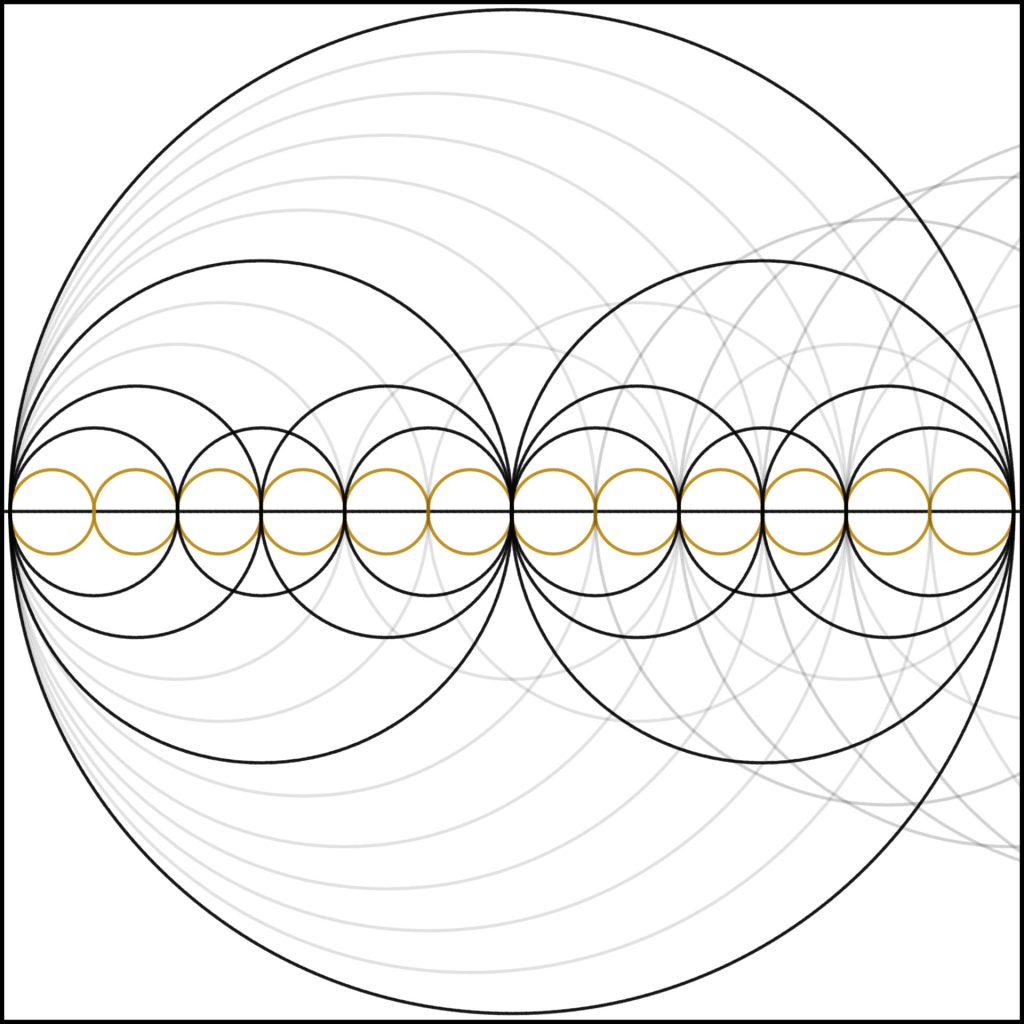
Step 12: And finally we come to 12. Note again the explosion in complexity compared to the prime number 11 and (can you guess what it looks like) the prime number 13 after.

Addendum: Interestingly, one can use this same model with fractions.If we define this largest circle in the related image (6) as 1, then the gold units are 1/6ths. We can easily see that three sixths equal a half, and that two thirds cannot be expressed in terms of halves. As we define larger and larger numbers as 1, we have fractions which race to infinity just as the number line races to infinity as we count upwards. An interesting symmetry.
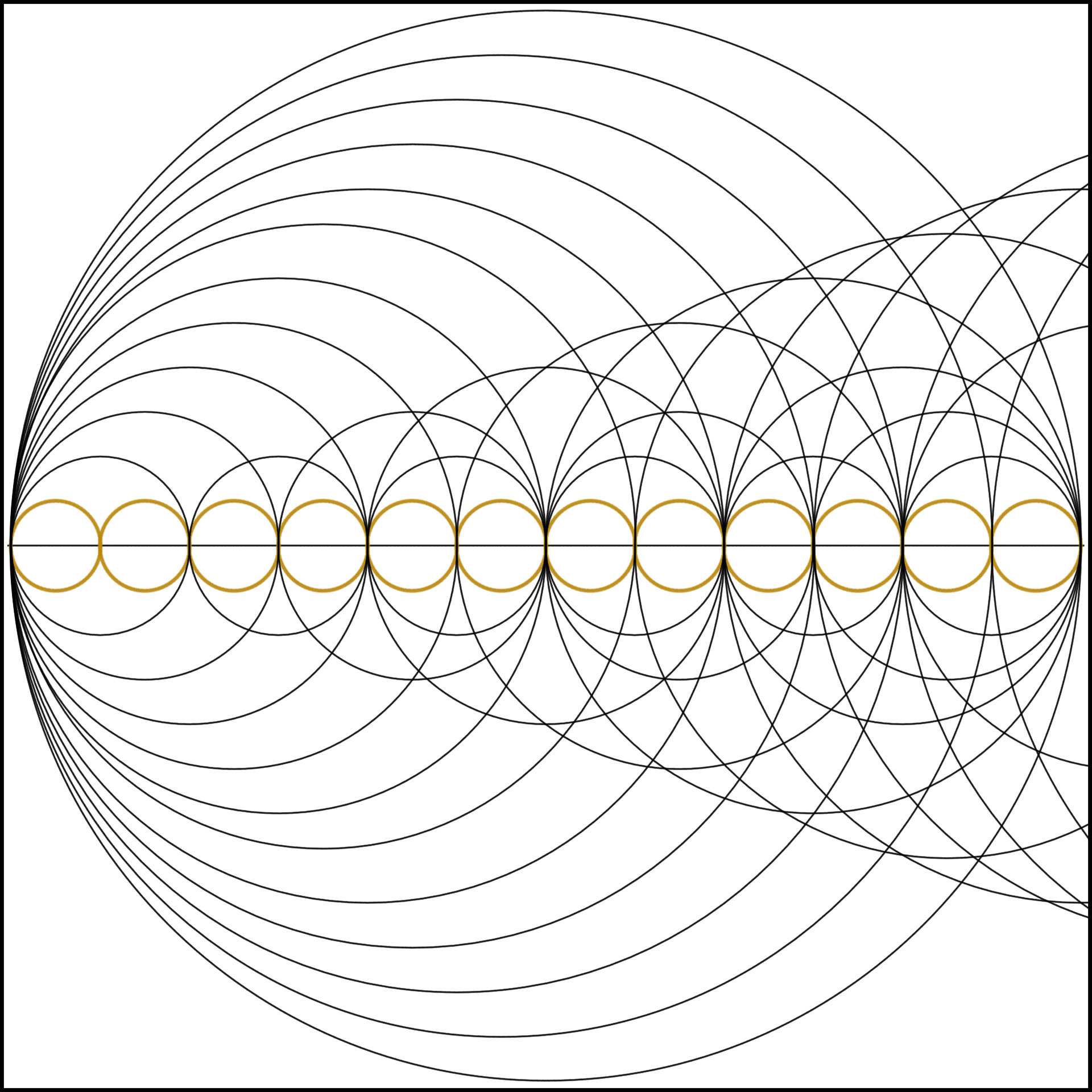
In addition to showing the internal structures of the numbers above, I hope you can also see the increasing complexity of the number line as we count upwards. Each new number sending a harmonic wave up the number line that dances with all the waves which came before it.
I hope that, to some degree, this not only only shows the inner structure of various numbers and number classes, but also hints at the complexities which may lurk higher up the number line. I hope the above sparks your curiosity as to what else may be out there.
I do have an app which I’ll post shortly which will create these numerical representations for you in your browser.
Please check back in the coming weeks if you wish to explore this further with me.
Finally, for anyone curious as to what the number line looks like with all harmonics up to 12 shown, please see the attached image.