So, we finished off with the Golden Triangle an earlier article. In this we will continue to explore the self-similar properties of this triangle in more detail.
Step 1: We start with our Golden Triangle (see earlier article here).
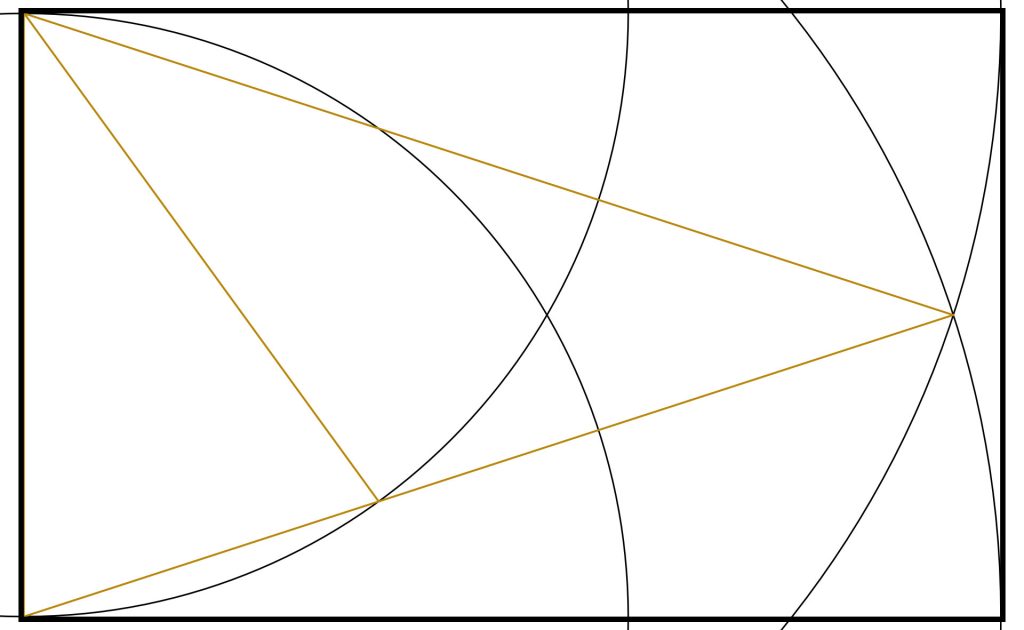
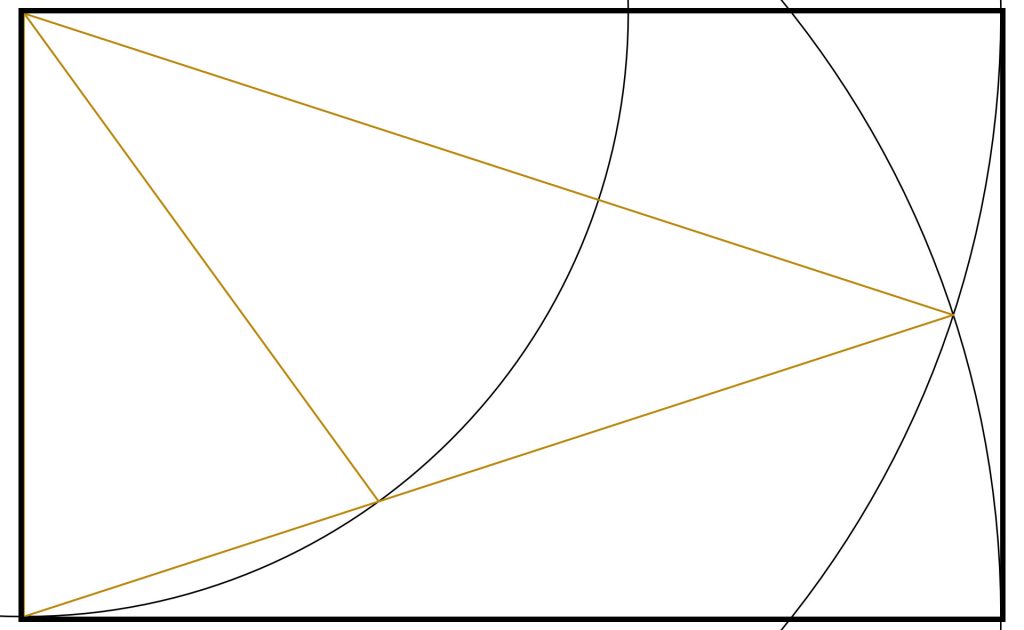
Step 2: Immediately we note that we could create a second internal Golden Triangle by repeating the steps me took before. This time we draw an arc from the bottom left with radius equal to the base of the original Golden Triangle.
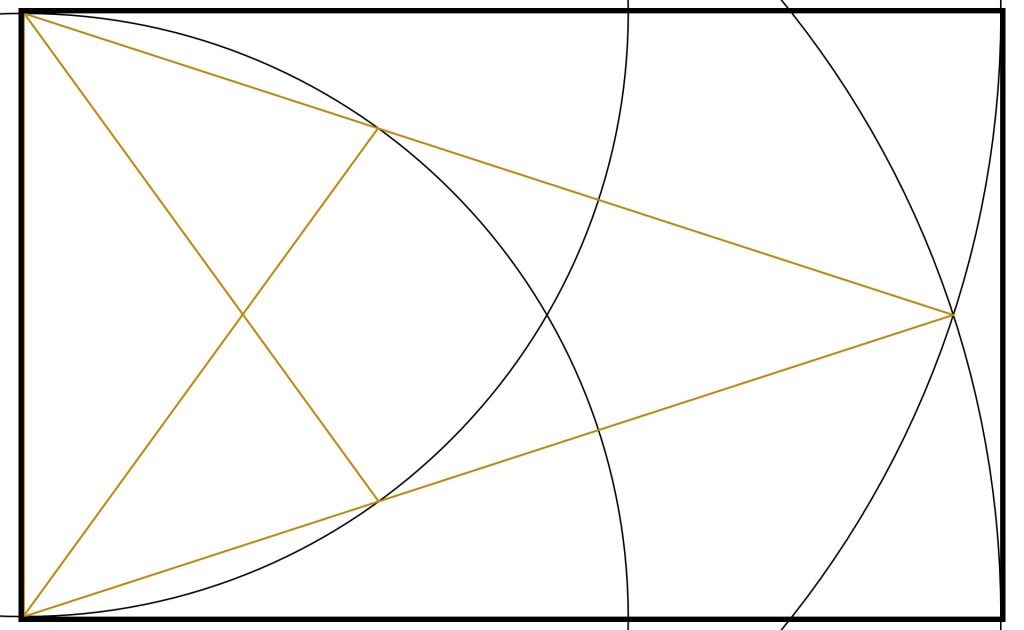
Step 3: We now connect the bottom left corner to where the arc crosses the top most line of the original golden triangle.
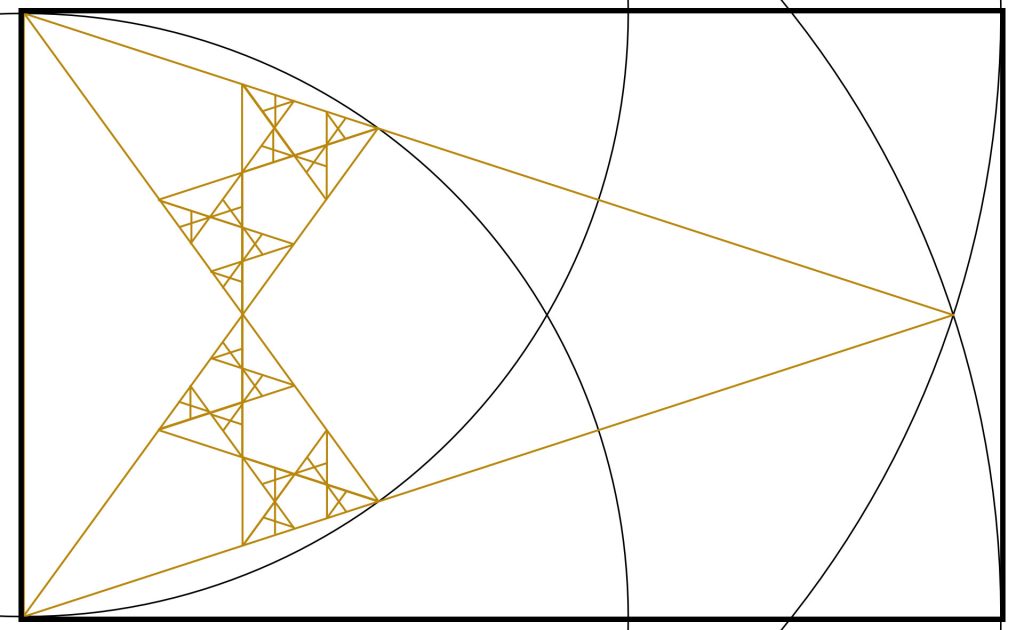
Step 4: We can clearly see that this action has already created two smaller Golden Triangles within the Golden Triangles at the base of our original Golden Triangle. We can continue this process into the triangles.
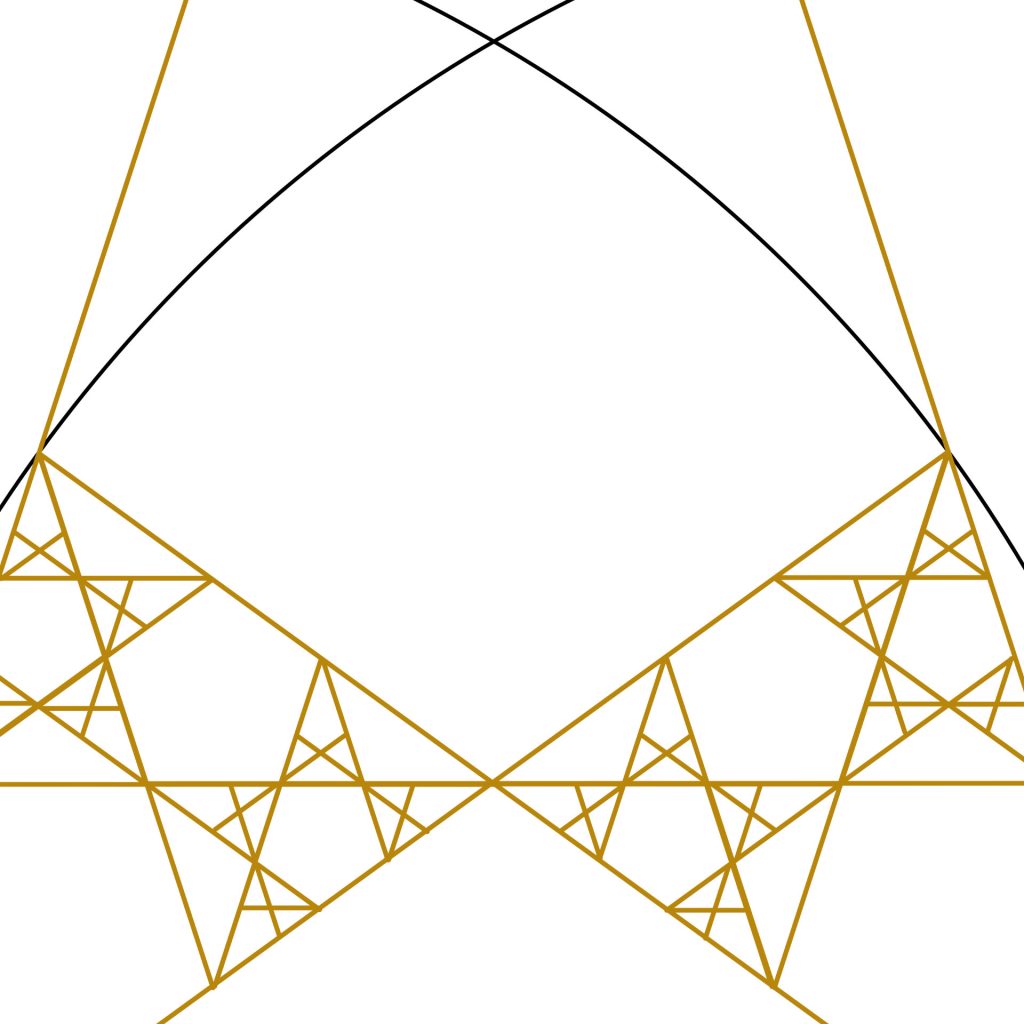
Step 5: We can now see an interesting pattern emerging. Within the smaller triangles we can now see a pattern of regular pentagons forming, with side lengths equal to the long and short sides of the Golden Triangles respectively.

Step 6: We see that the pentagons form pentangle patterns with the Golden Triangles. Could we create a pentagon in our golden triangle?
Can you guess where?
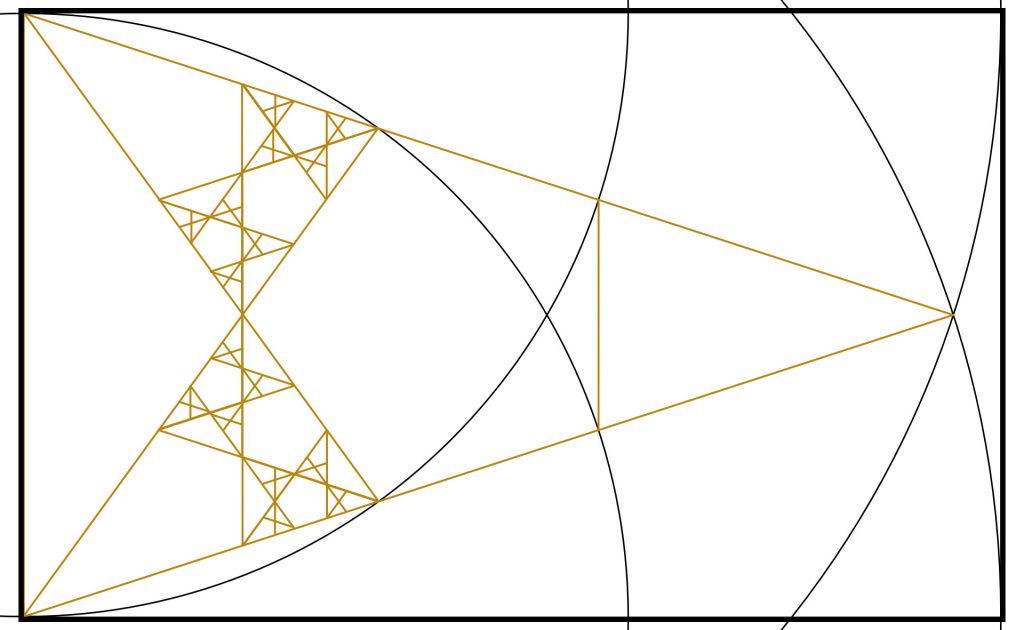
Step 7:
Yes, we just connect the second intersections our arcs made earlier. We now have our top Golden Triangle.

Step 7: We can complete the top Golden Triangle just as we did the bottom ones.
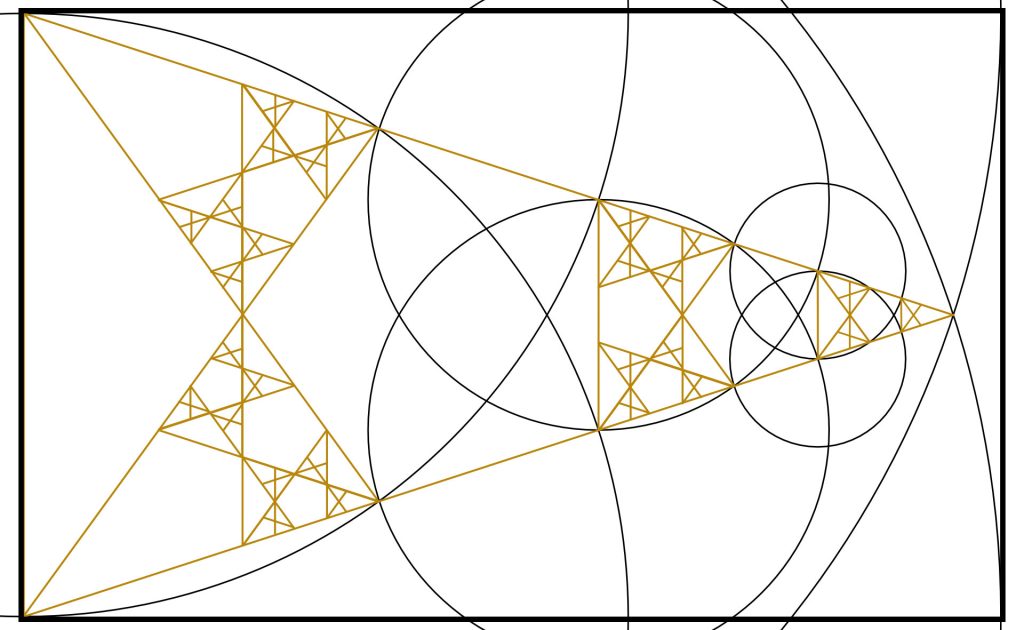
Step 8: It is now obvious that we can also add more Golden Triangles into the top of our existing smaller Triangles.
I have completed the top with construction lines shown for clarity.
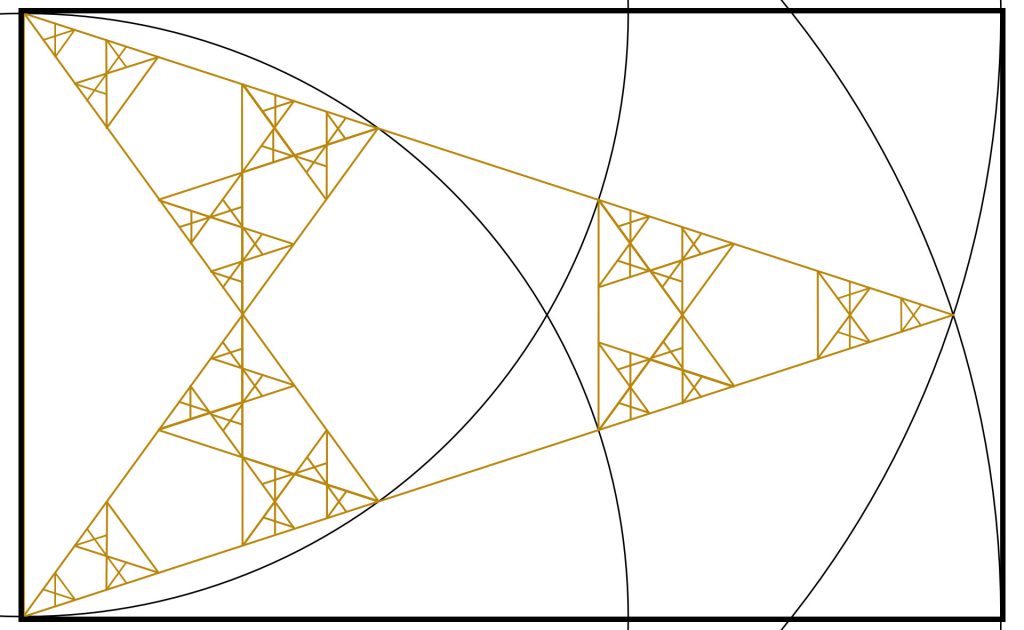
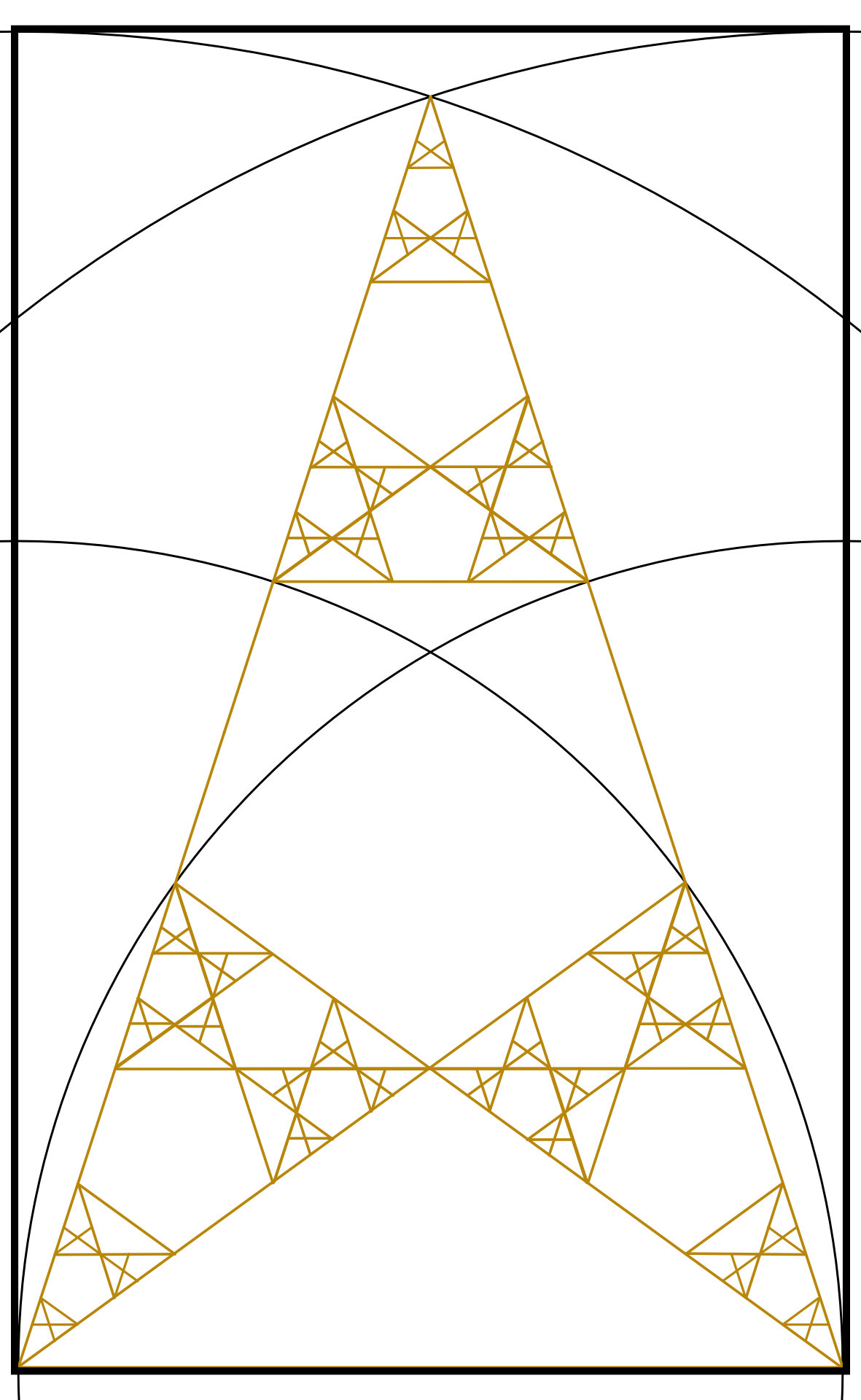
Step 9: We can now do the same for the bottom remaining two Golden Triangles completing the Golden Triangle (to this many generations). This is a fractal structure based on an irrational number so it is still only an approximation.
AFTERTHOUGHTS AND FUTURE STUDIES: So now we’ve come to the end of this study of the Golden Triangle we have found that from the harmonic repetition of the Golden Ratio we have created regular pentagons and other structures with our Triangle. We have also seen how it exhibits fractal qualities continuing on forever. We will be looking at both of these matters in later articles.
Also, I will be going through various proofs of all discussed here, but for now I am trying to keep it simple and as non-technical as possible. So simple a child could understand. I hope that this makes it more accessible and enjoyable to study.
NB: It should be noted that I have not filled in all possible Golden Triangles in this exercise. We will be coming back to the Golden Triangle once we have looked at Pentagons in more detail.
Here is a larger version of the completed Golden Triangle if you are interested.