In this article we will be looking at how the simple regular pentagon is in fact recursively resonant with Φ (Phi), the Golden Ratio. This article will rely on an understanding of the Golden Triangle which can be found in this article.
The Golden Triangle can be created from a Golden Rectangle as described here, and a regular pentagon can be constructed from scratch as described here.

STEP 1: We start with a regular pentagon.
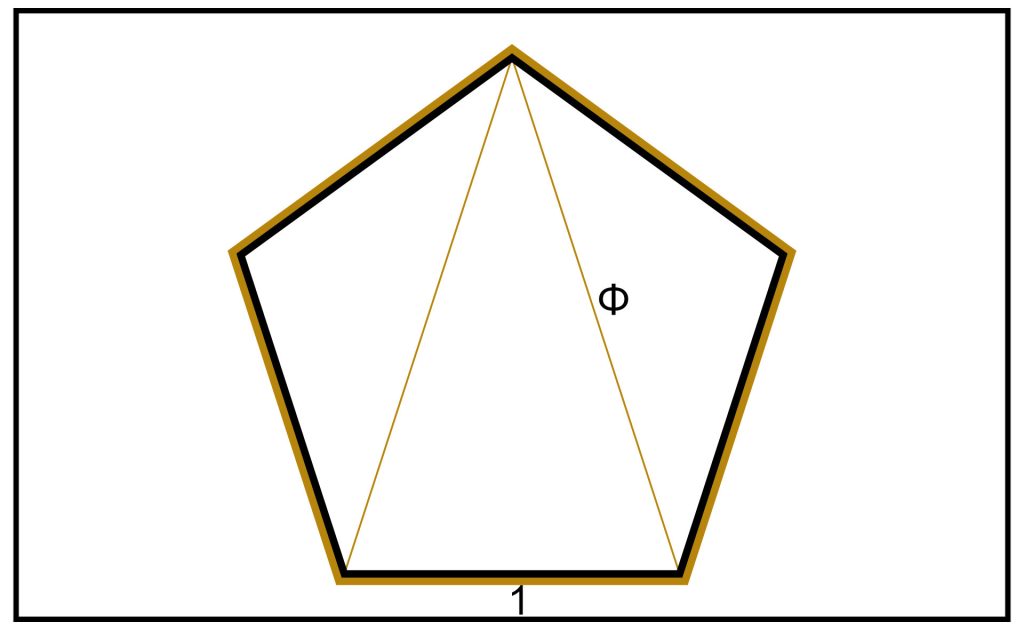
STEP 2: We draw two diagonals from the bottom left and right corners to the only point they are not connected to. The top.
We immediately have a Golden Triangle and two Golden Gnomons either side of the Golden Triangle.
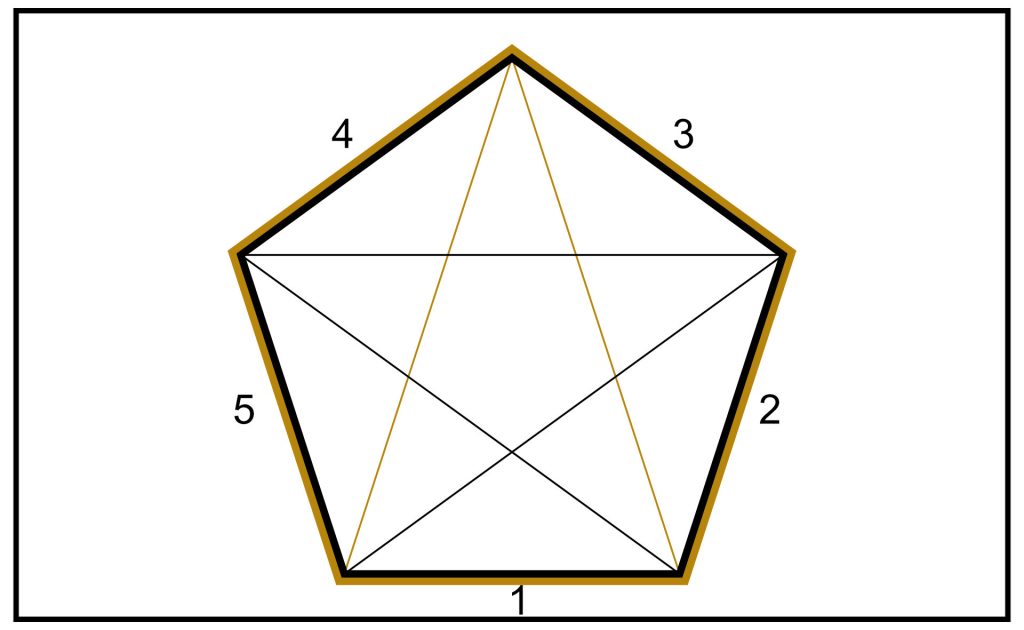
STEP 3: We draw in the remaining diagonals, creating the five pointed star, the Pentagram.
The base of each of the five Golden Triangles is numbered accordingly. The original Golden Triangle remains in gold so you can observe that a simple rotation around the centre will give you the other four Golden Triangles. They are all identical.
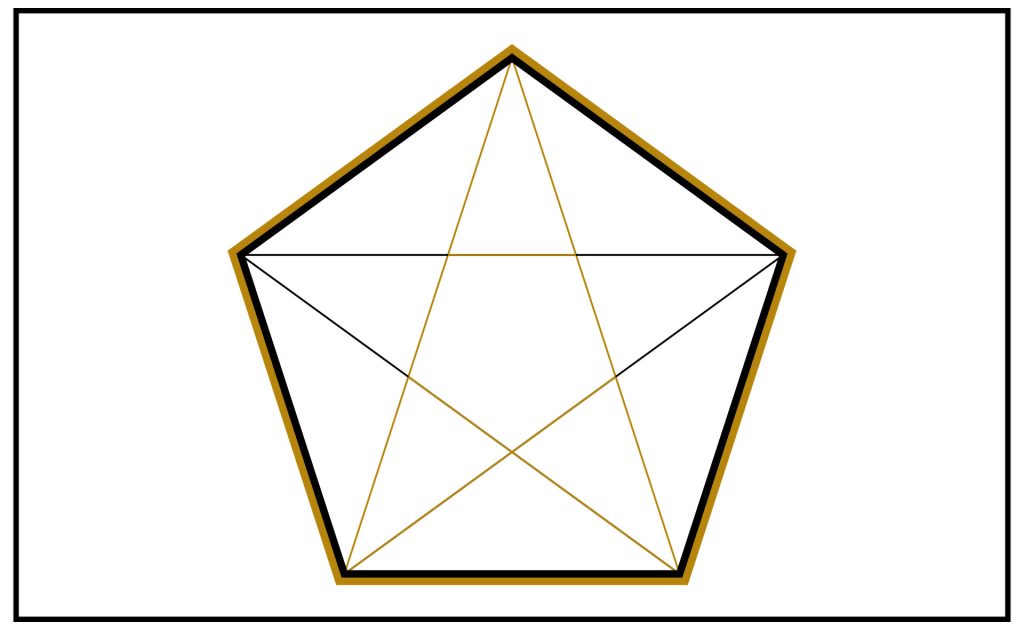
STEP 4: We now turn our attention to the original Golden Triangle.
We see that the diagonal lines we have drawn have perfectly broken down the original Golden Triangle into resonant smaller Golden Triangles and Golden Gnomons.
We also note the inverted pentagon in the middle.
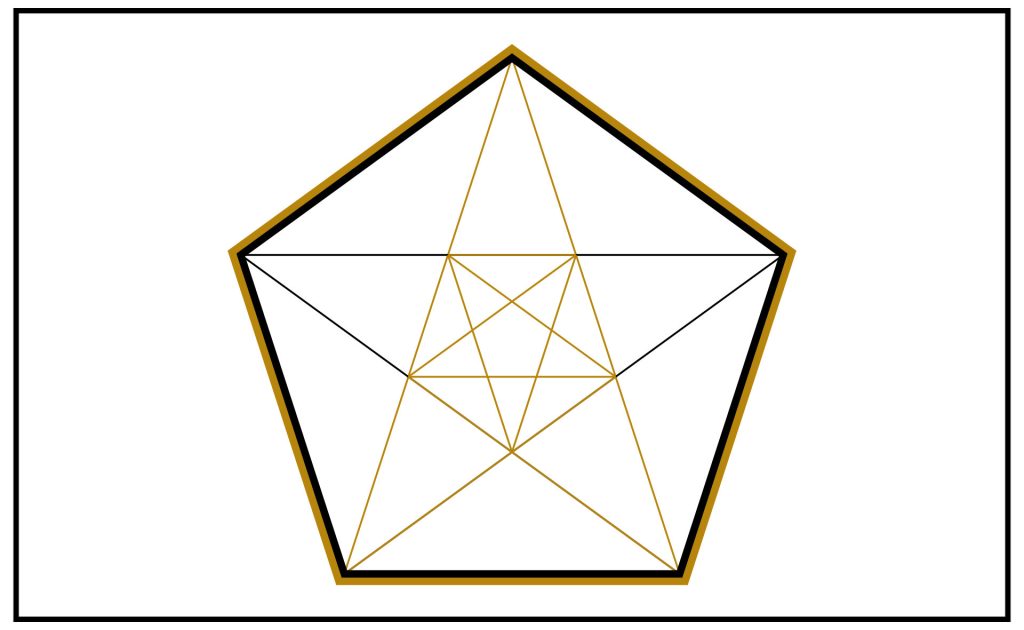
STEP 5: We can, of course, repeat the above with the central inverted pentagon giving us the next generation of Golden Gnomons and Golden Triangles.
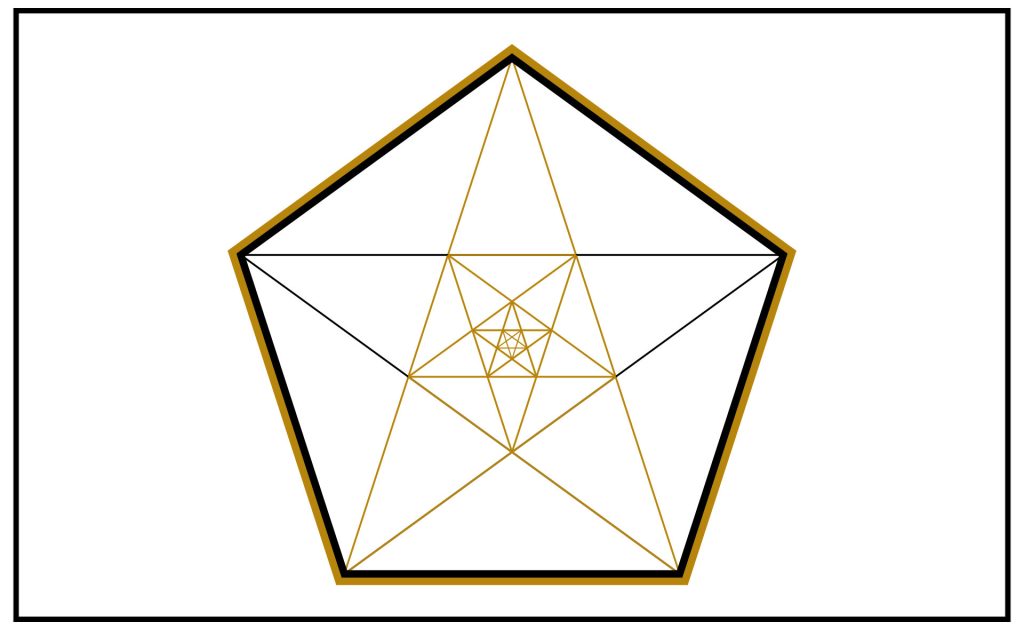
STEP 6: This process could be repeated infinitely giving us Golden Triangles and Gnomons repeatedly down to infinity.
I have drawn a few levels deep to illustrate the concept.
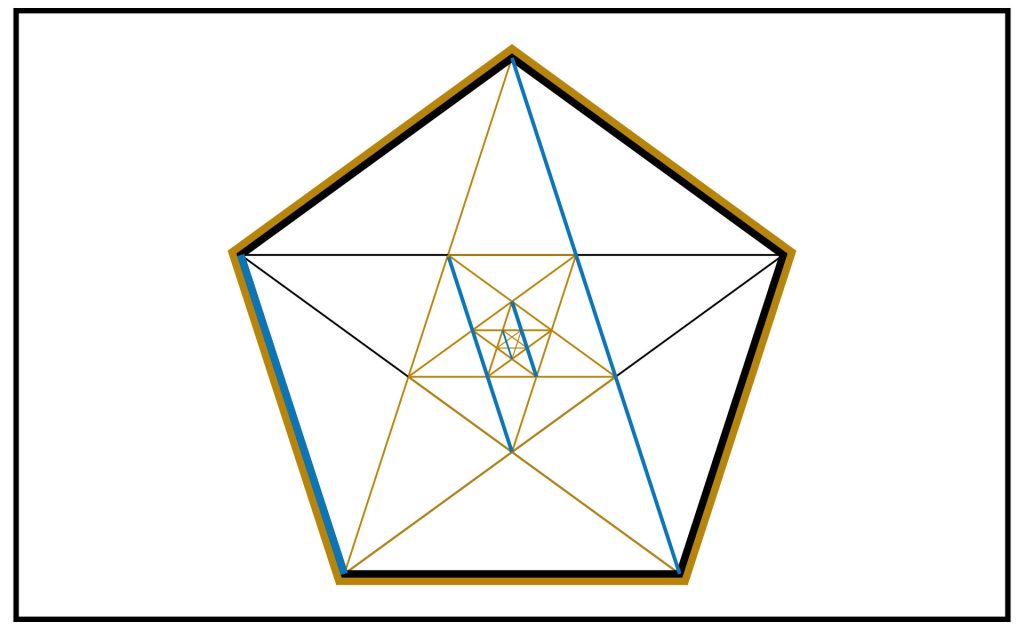
STEP 7: Whilst this is interesting, it gets very small very fast. We need a way of determining the resonances in a more general fashion.
To do this we notice how all the lines used so far are parallels to the existing sides of the outer pentagon. One such series of parallel lines is shown in blue here.
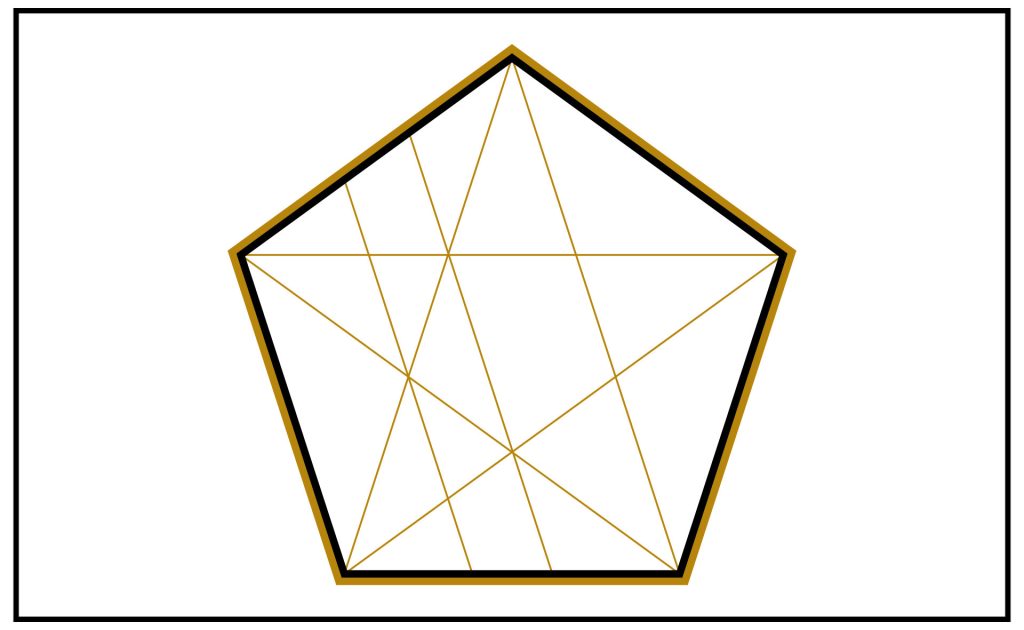
STEP 8: Now we know that all the lines are parallels of the original sides of the pentagon and that the nodes (where the diagonals cross) are themselves points resonant with Phi, we now draw parallel lines through all the nodes available.
I have done one series of parallels here to illustrate.
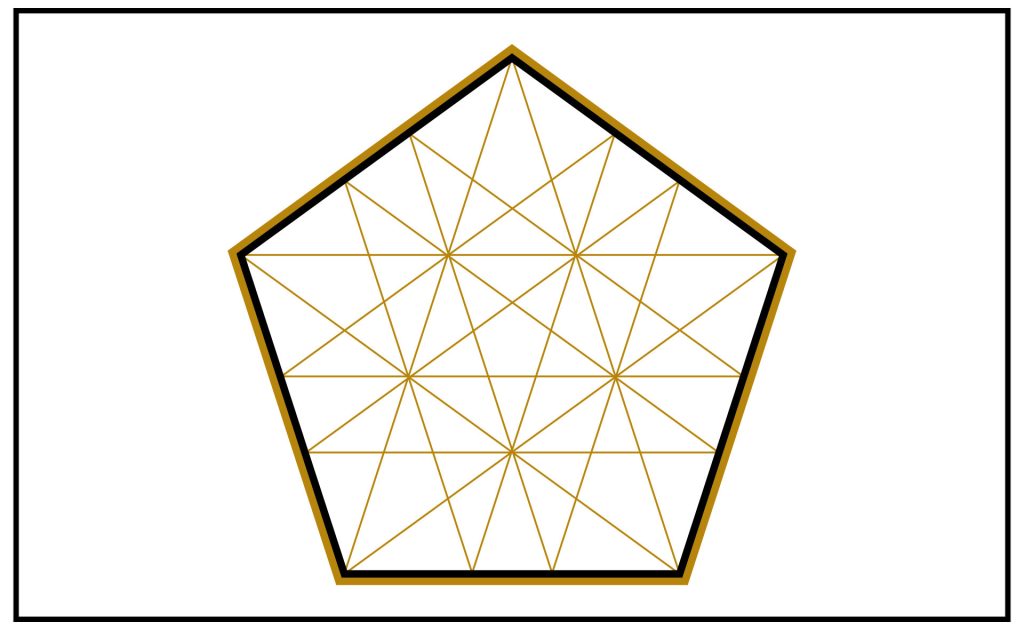
STEP 9: We repeat this for all the sides of the pentagon. This is the resultant structure. We have, of course, recreated the inverted pentagram in the centre.
This process has also created a new set of nodes which we can again use to create the parallels.

STEP 10: We repeat this for the newly emerged nodes. This is the second generation of harmonics and we can see the familiar small pentagram born in the centre.
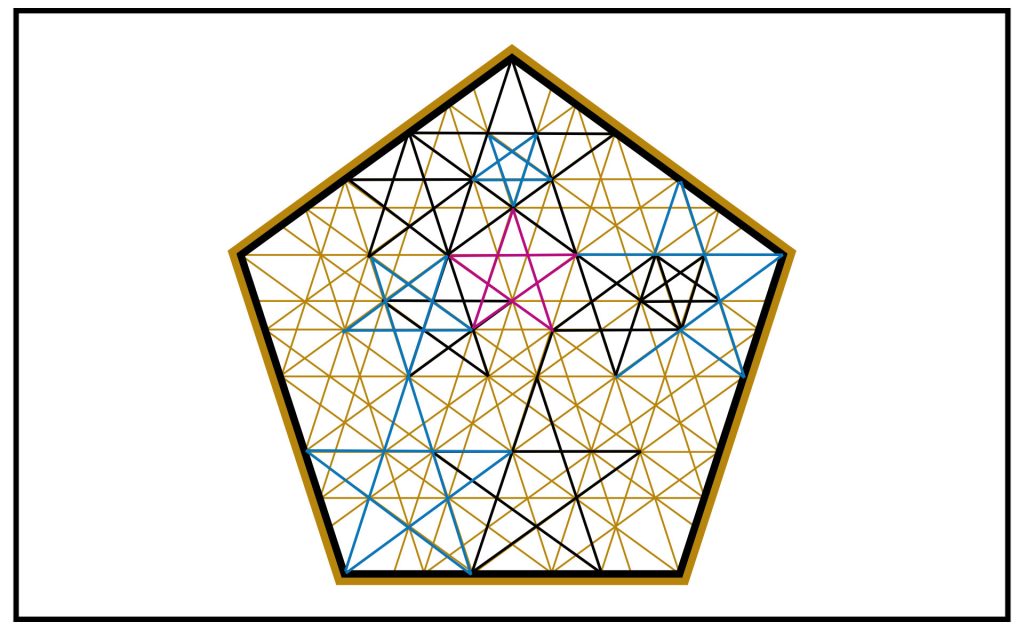
STEP 11: If you look carefully, you can see we are beginning to create an interesting fractal pattern based around Φ (Phi).
After only two harmonic generations you can see a myriad of recursive pentagrams forming, all related to each other by Phi. I have outlined a few of them in in the attached image for clarity. This would only get more complex should we continue this process.
From the above you can see that the regular pentagon is itself infinitely harmonic with Φ (Phi), the golden ratio. Sadly it becomes increasingly hard to draw accurately in each new generation. We will come back to this structure programatically in later articles for a closer look.
I do find it interesting that in our modern culture we associate the pentagram most closely with satanism. It is a geometrically perfect self-similar representation of Φ (Phi). One could argue that the view that this sign signifies evil is, in fact, a total inversion of mathematical and objective reality. Perhaps someone was trying to hide something.