Now that we have the Golden Rectangle to hand, we can start exploring other geometric shapes with similar properties. One of the most obvious examples would be the Golden Triangle. The Golden Triangle can be constructed as follows.

Step 1: Start with a Golden Rectangle (See here if you need to construct one).
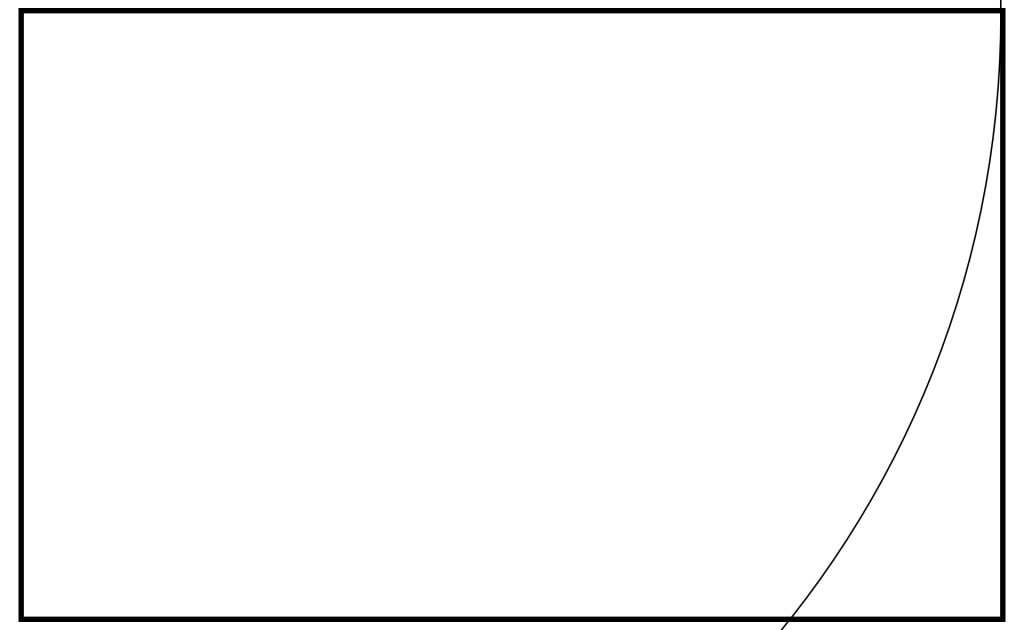
Step 2: Draw an arc from the top right corner with radius equal the width of the rectangle to that it intersects the top right angle.

Step 3: Do the same from the bottom right corner, making sure the arc is also of a radius equal to the width of the Golden Rectangle.
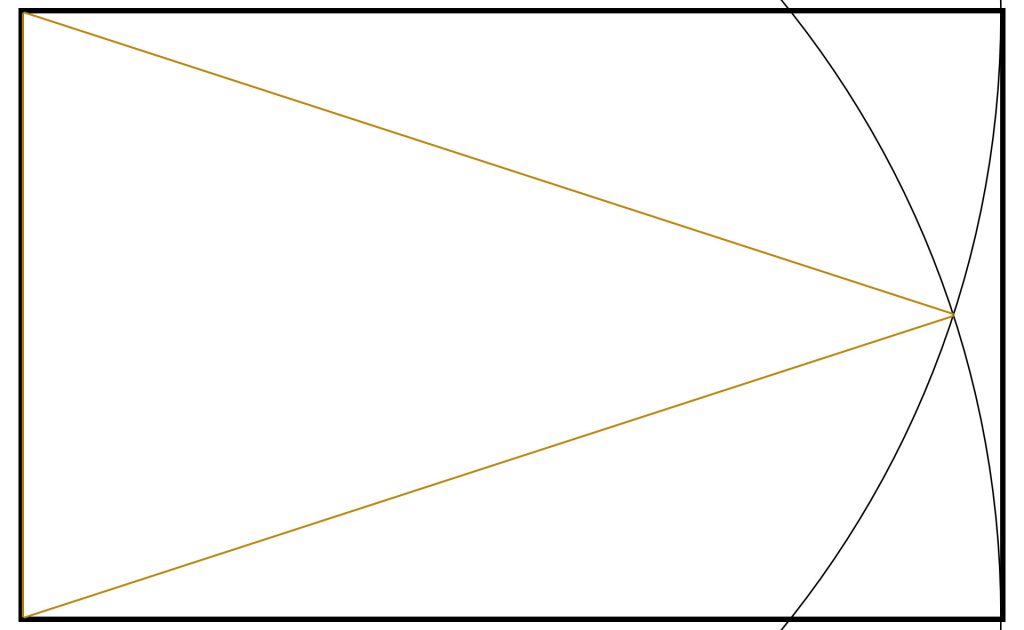
Step 4: Draw a line from where the circles intersect to each of the left hand corners of the Golden Rectangle. The resultant isosceles triangle is a Golden Triangle.
CREATING INTERNAL GOLDEN TRIANGLES
Now that we have a Golden Triangle we can, in similar fashion to how we did with the Golden Rectangle, find a proportionally smaller triangle which is also a Golden Triangle in a single step. This can be repeated indefinitely mathematically and as far as the accuracy of our original Golden Rectangle allows practically.
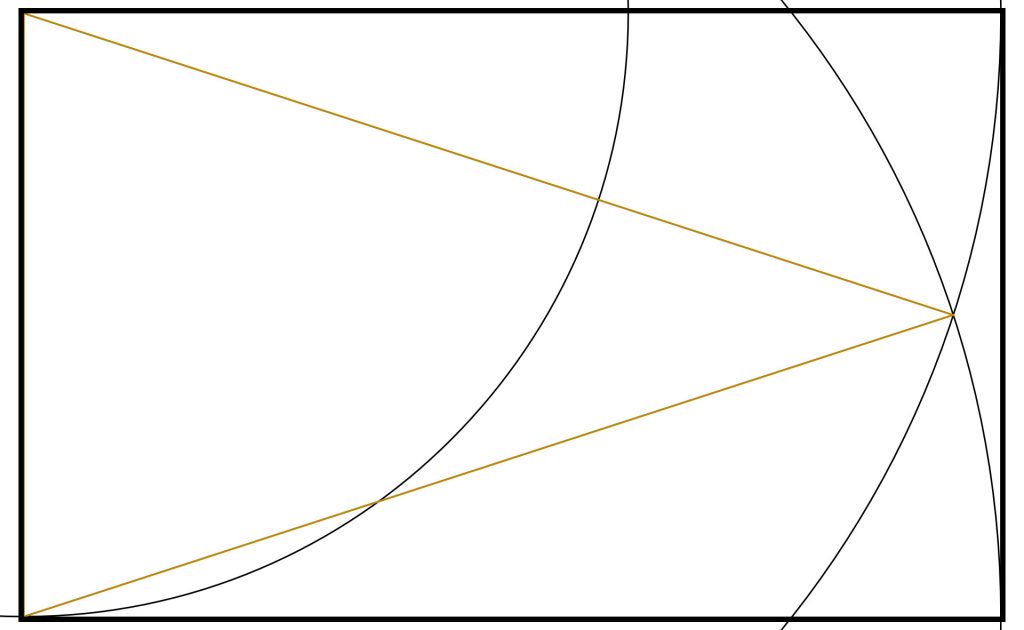
Step 5: To create an internal Golden Triangle, just draws and arc from the top right of the Golden Triangle with a radius equal to the base.
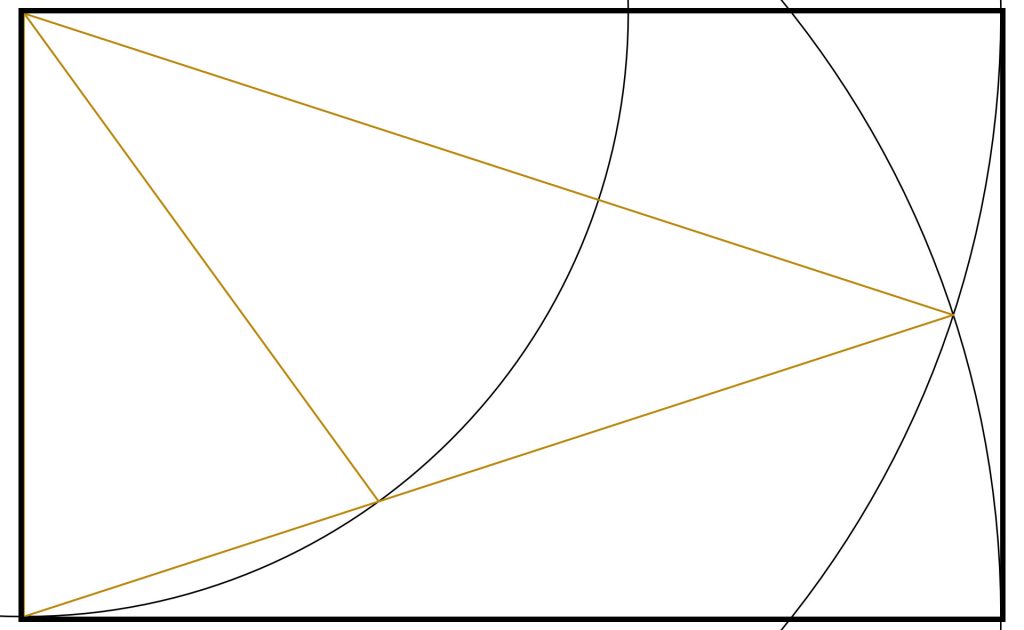
Step 6: Connect the top right to the point where the arc crosses the Golden Triangle.
This is a basic introduction to the Golden Triangle. For a more in depth look please see the next article in this series.
RELATED LINKS