To construct and understand the Golden Rectangle it is necessary to understand a few basic concepts. These are the Fibonacci sequence and Φ (Phi), also known as the ‘Golden Ratio’ and the ‘Divine Proportion’ as well as many other names. These will be discussed briefly below but will be explored more fully in future posts.
THE FIBONACCI SEQUENCE
The Fibonacci sequence, as it is currently know, has been known since before antiquity. It can be constructed easily starting from 0 and 1 such that each number is the sum of the two preceding ones.
The first eleven Fibonacci numbers (Fn) Fibonacci sequence can shown as follows and continue on to infinity.
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F… | F∞ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | … | ∞ |
Φ (PHI) AND THE GOLDEN RATIO
The ratios between any two numbers in this sequence tend towards Φ, the Golden ratio or the divine proprtion. Φ has a value of 1.618… and 1/Φ has a value of 0.618… . Both of these numbers can be seen to emerge from the ratio of any adjacent Fibonacci numbers. This will be discussed at length elsewhere.
| Pair | F1:F2 | F2:F3 | F3:F4 | F4:F5 | F5:F6 | F6:F7 | F7:F8 | F8:F9 | F9:F10 | F10:F11 |
|---|---|---|---|---|---|---|---|---|---|---|
| Fn+1/Fn | 1 | 2 | 1.5 | 1.66 ̇ | 1.6 | 1.625 | 1.615… | 1.619… | 1.618… | 1.618… |
| Fn/Fn+1 | 1 | 0.5 | 0.66 ̇ | 0.6 | 0.625 | 0.615… | 0.619… | 0.618… | 0.61 ̇8 ̇ | 0.618… |
STEP 1: We start with the first ‘1’ in the sequence. Next to this we add the next number, another ‘1’. This gives us our worst approximation of the Golden Rectangle with Phi and 1/Phi as approximately 1.
STEP 2: Next we add the second one from the Fibonacci sequence. We now have an actual rectangle of width 2, height 1. This, again, gives us a very rough value of Phi as being 1.5. Still, we are closer than before.
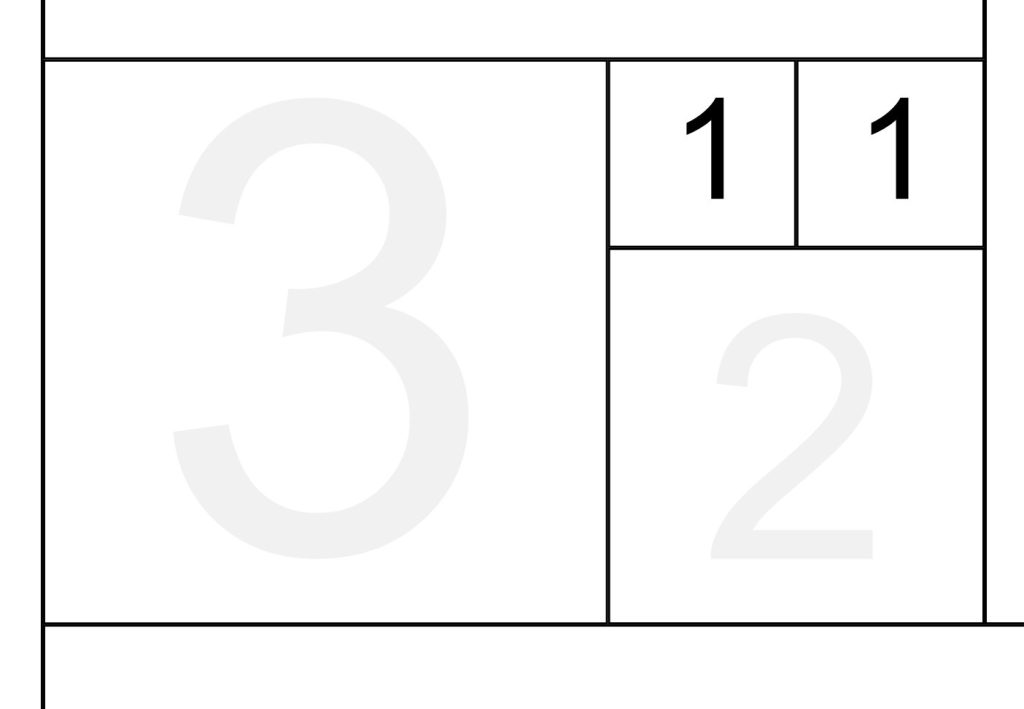
STEP 3: We continue this process and create a rectangle of 2:3 (Phi of 1.66…) and then onwards to a rectangle of 5:3, giving Phi of exactly 1.6.
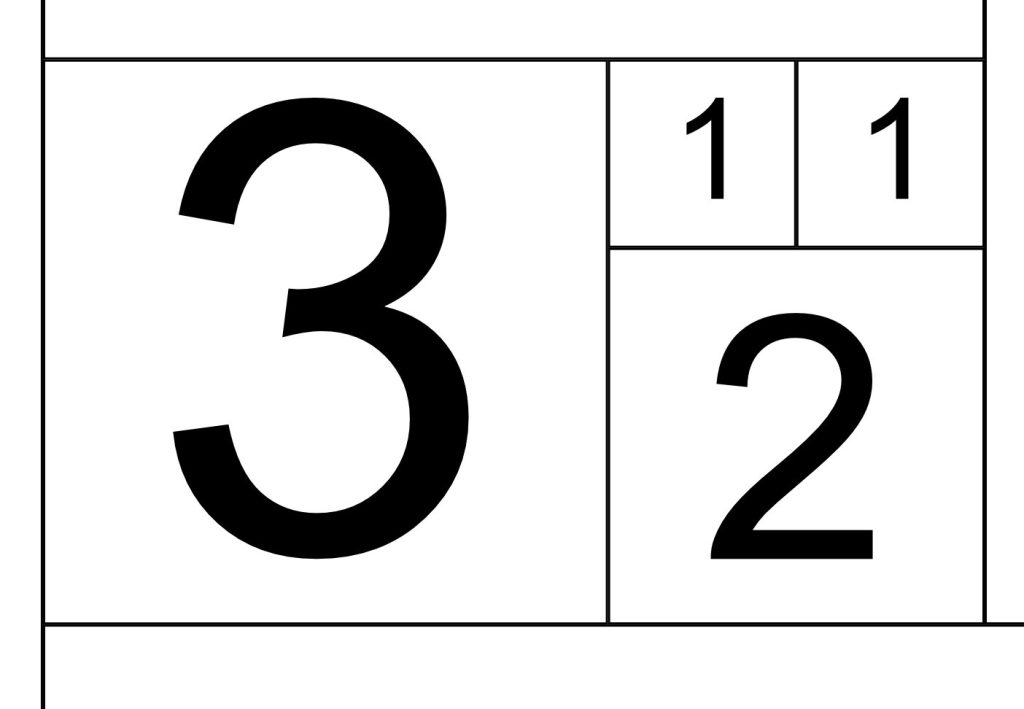
STEP 4: At this point I hope you begin to get a feeling for the self similar nature of this structure as we increase in size. Look how small the 2:1 rectangle is getting. This is the key to understanding phi. This geometrical structure is beginning to exhibit scale invariance.

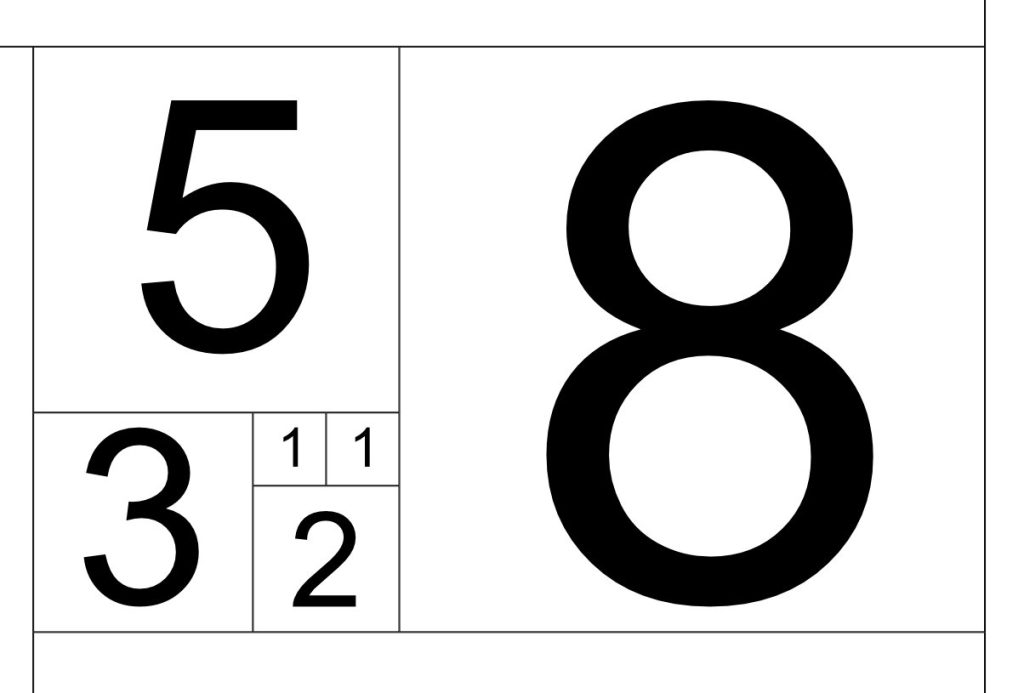
STEP 5: By this stage I imagine you understand how this process operates and I just want to flag the speed at which this process is escaping from the original 2:1 rectangle in STEP 2 above. In this step, for example, the last square we added was 21×21. 21 times larger than the original 1×1 square.
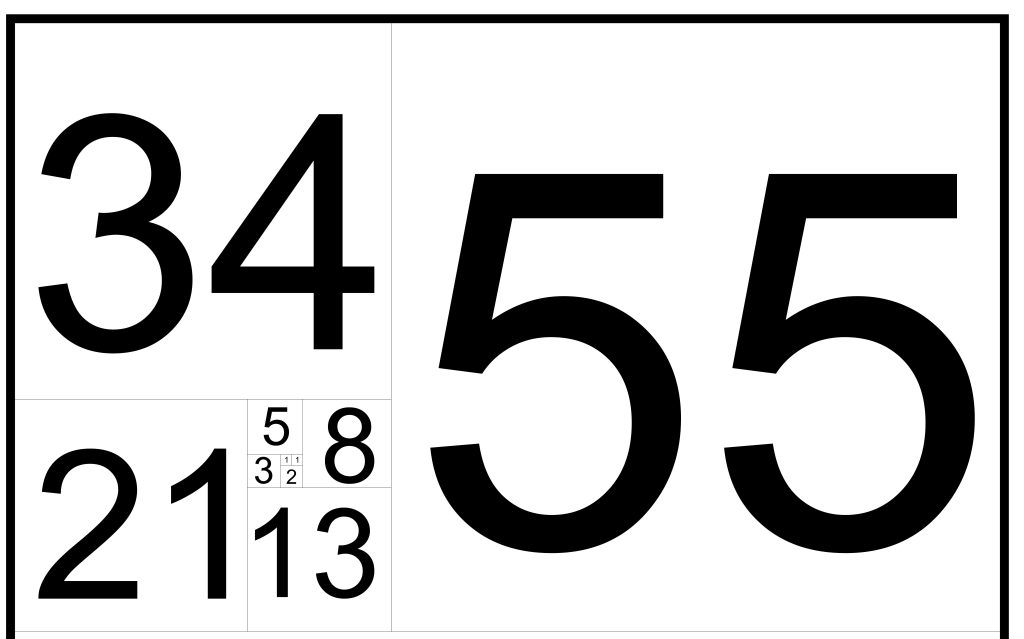
STEP 6: Again, just to illustrate the point further, our last added square in this example is 55×55, so roughly a 2.6x (approx. Φ2) increase in the speed at which we’re flying away from the original 1×1 square compared to a two steps earlier.
THE COMPLETED GOLDEN RECTANGLE (UP TO 89)
We have finally forged our Golden Rectangle (accurate to three decimal places).

Of course, by this point I’m sure you realise that the numbers mean little as we race away from the original starting blocks. What is important is that we can now see the proportions what give rise to this process more clearly than when we started.
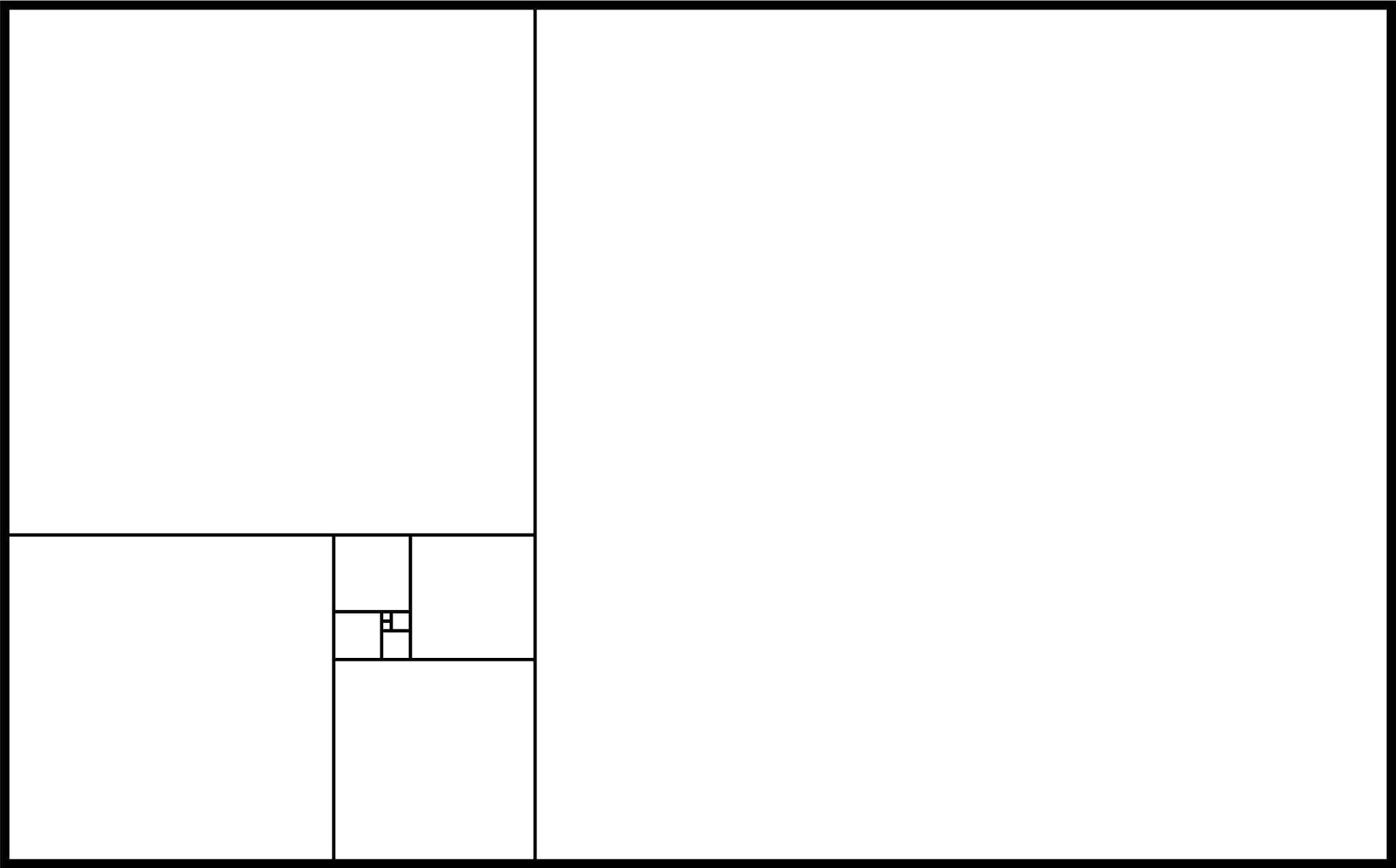
From here we can now create an approximation of the golden spiral.
Whilst this is an adequate approximation for the Golden Rectangle for most purposes (and becomes increasingly so as we increase in size), it is not nor ever will be the true Golden Rectangle.
As Phi is irrational, and, as some say, the most irrational of the irrationals, we can never create a true Golden Rectangle, only a more and more accurate approximation of it.
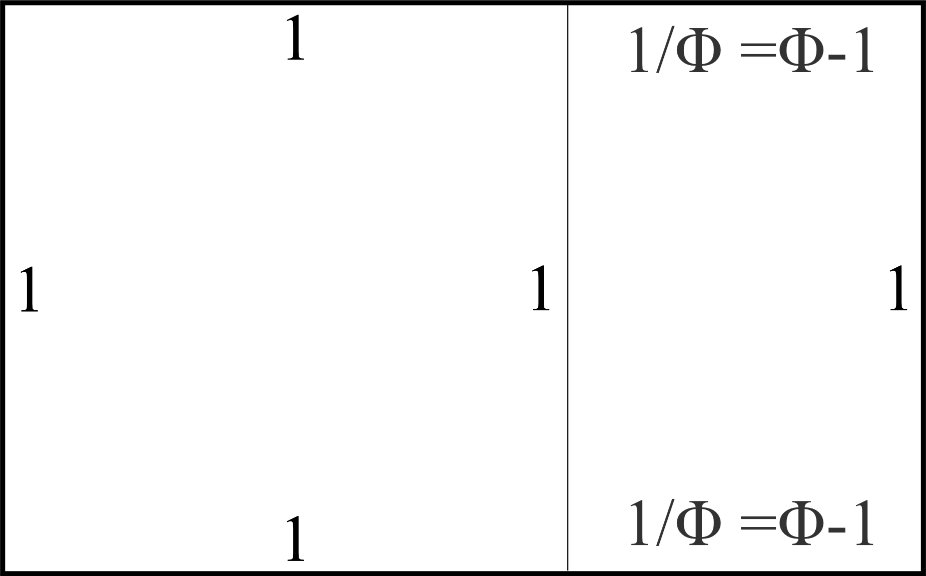
The real Golden Rectangle, which can only be roughly represented with the image above, is perfectly self-similar in every generation up and down, always giving rise to a rectangle with the perfect proportions as it races both to from infinity. It would be a simple example of a self generating mathematical process which is without beginning and without end. In some ways it is similar to what we would now call a fractal. Personally, when contemplating this, it reminds me of the childhood experience of holding a candle between two mirrors, but in this case one feels as if one can glimpse the enormity of eternity. If you hit the quintillions, just keep on going.
The mere 100th Fibonacci number is 354,224,848,179,261,915,075, or 354 quintillion odd, just to give the impression of how fast this sequence escalates. And it continues accelerating from there. It is beyond astronomical, and close to the bounds of beyond cosmological. And we have barely scratched the surface.
The fact that this pattern emerges time and again in nature (via the Golden Spiral), in everything from eddies and whirlpools to flowers, tropical cyclones and (to our eyes) the structure of galaxies would only serve to further the wonder people must have felt when they first became aware of this. The Pythagoreans were famous for their love of this process, using it as the core of their sacred symbol. We will discuss this in more detail when looking at the Golden Triangle.